
【题目】设![]() ,数列
,数列![]() 满足
满足![]() ,
,![]()
![]() .
.
(Ⅰ)当![]() 时,求证:数列
时,求证:数列![]() 为等差数列并求
为等差数列并求![]() ;
;
(Ⅱ)证明:对于一切正整数![]() ,
,![]() .
.
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
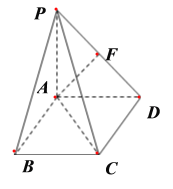
【题目】如图,四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为2的正方形,
PA=AD,F为PD的中点.
(1)求证:AF⊥平面PDC;
(2)求直线AC与平面PCD所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
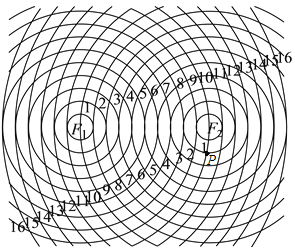
【题目】已知,如图, ![]() ,图中的一系列圆是圆心分别为
,图中的一系列圆是圆心分别为![]() ,
, ![]() 的两组同心圆,每组同心圆的半径依次为
的两组同心圆,每组同心圆的半径依次为![]() ,
, ![]() ,
, ![]()
![]() ,
,
按“加![]() ”依次递增,点
”依次递增,点![]() 是某两圆的一个交点,设:
是某两圆的一个交点,设:
以![]() ,
, ![]() 为焦点,且过点
为焦点,且过点![]() 的椭圆为
的椭圆为![]() ;
;
以![]() ,
, ![]() 为焦点,且过点
为焦点,且过点![]() 的双曲线为
的双曲线为![]() ,
,
则
(![]() )双曲线
)双曲线![]() 离心率
离心率![]() __________.
__________.
(![]() )若以
)若以![]() 为
为![]() 轴正方向,线段
轴正方向,线段![]() 中点为坐标原点建立平面直角坐标系,则
中点为坐标原点建立平面直角坐标系,则
椭圆![]() 方程为__________.
方程为__________.
(3)双曲线![]() 渐近线方程为__________.
渐近线方程为__________.
(4)在两组同心圆的交点中,在椭圆![]() 上的点共__________个.
上的点共__________个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在每年的3月份,濮阳市政府都会发动市民参与到植树绿化活动中去林业管理部门为了保证树苗的质量都会在植树前对树苗进行检测,现从甲、乙两种树苗中各抽测了![]() 株树苗,量出它们的高度如下(单位:厘米),
株树苗,量出它们的高度如下(单位:厘米),
甲:37,21,31,20,29,19,32,23,25,33;
乙:10,30,47,27,46,14,26,10,44,46.

(1)画出两组数据的茎叶图并根据茎叶图对甲、乙两种树苗的高度作比较,写出两个统计结论;
(2)设抽测的![]() 株甲种树苗高度平均值为
株甲种树苗高度平均值为![]() ,将这
,将这![]() 株树苗的高度依次输人,按程序框(如图)进行运算,问输出的
株树苗的高度依次输人,按程序框(如图)进行运算,问输出的![]() 大小为多少?并说明
大小为多少?并说明![]() 的统计学意义,
的统计学意义,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项![]() (a是常数),
(a是常数),![]() (
(![]() ).
).
(1)求![]() ,
,![]() ,
,![]() ,并判断是否存在实数a使
,并判断是否存在实数a使![]() 成等差数列.若存在,求出
成等差数列.若存在,求出![]() 的通项公式;若不存在,说明理由;
的通项公式;若不存在,说明理由;
(2)设![]() ,
,![]() (
(![]() ),
),![]() 为数列
为数列![]() 的前n项和,求
的前n项和,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)如图,长方形材料![]() 中,已知
中,已知![]() ,
,![]() .点
.点![]() 为材料
为材料![]() 内部一点,
内部一点,![]() 于
于![]() ,
,![]() 于
于![]() ,且
,且![]() ,
,![]() . 现要在长方形材料
. 现要在长方形材料![]() 中裁剪出四边形材料
中裁剪出四边形材料![]() ,满足
,满足![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() ,
,![]() 上.
上.
(1)设![]() ,试将四边形材料
,试将四边形材料![]() 的面积表示为
的面积表示为![]() 的函数,并指明
的函数,并指明![]() 的取值范围;
的取值范围;
(2)试确定点![]() 在
在![]() 上的位置,使得四边形材料
上的位置,使得四边形材料![]() 的面积
的面积![]() 最小,并求出其最小值.
最小,并求出其最小值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马, 田忌的下等马劣于齐王的下等马.现从双方的马匹中随机选一匹进行一场比赛,则田忌的马获胜的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com