
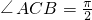 .以直线AC为轴旋转一周得到一个圆锥,D为圆锥底面一点,BD⊥CD,CH⊥AD于点H,M为AB中点,则当三棱锥C-HAM的体积最大时,CD的长为
.以直线AC为轴旋转一周得到一个圆锥,D为圆锥底面一点,BD⊥CD,CH⊥AD于点H,M为AB中点,则当三棱锥C-HAM的体积最大时,CD的长为
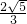


 S△CMH×AM,因此当S△CMH达到最大值时,三棱锥C-HAM的体积最大.设∠BCD=θ,利用Rt△ACD中等积转换和Rt△ABD∽Rt△AHM,算出CH、HM关于θ的式子,从而得到S△CMH=
S△CMH×AM,因此当S△CMH达到最大值时,三棱锥C-HAM的体积最大.设∠BCD=θ,利用Rt△ACD中等积转换和Rt△ABD∽Rt△AHM,算出CH、HM关于θ的式子,从而得到S△CMH= CH•HM=
CH•HM= ,最后根据基本不等式得当tanθ=
,最后根据基本不等式得当tanθ= 时,S△CMH达到最大值,根据同角三角函数的基本关系算出cosθ=
时,S△CMH达到最大值,根据同角三角函数的基本关系算出cosθ= ,从而得出CD的长为
,从而得出CD的长为 ,即为当三棱锥C-HAM的体积最大时CD的长.
,即为当三棱锥C-HAM的体积最大时CD的长. 根据题意,得
根据题意,得 S△CMH×AM=
S△CMH×AM= S△CMH
S△CMH AB=
AB=
 ,BD=
,BD=
 =
=
 ,所以HM=
,所以HM= =
=
 CH•HM=
CH•HM= =
=
 tanθ,
tanθ, ≤
≤ =
= ,
, 时,S△CMH达到最大值,三棱锥C-HAM的体积同时达到最大值.
时,S△CMH达到最大值,三棱锥C-HAM的体积同时达到最大值. >0,可得sinθ=
>0,可得sinθ= cosθ>0
cosθ>0 ,可得cosθ=
,可得cosθ= (舍负)
(舍负) =
= ,
,


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源:大连一模 题型:单选题
| π |
| 2 |
A.
| B.
| C.
| D.
|
查看答案和解析>>
科目:高中数学 来源:2013年辽宁省大连市高考数学一模试卷(理科)(解析版) 题型:选择题
 .以直线AC为轴旋转一周得到一个圆锥,D为圆锥底面一点,BD⊥CD,CH⊥AD于点H,M为AB中点,则当三棱锥C-HAM的体积最大时,CD的长为( )
.以直线AC为轴旋转一周得到一个圆锥,D为圆锥底面一点,BD⊥CD,CH⊥AD于点H,M为AB中点,则当三棱锥C-HAM的体积最大时,CD的长为( )



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com