
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§ΒΞΈΜ‘≤O”κy÷αΗΚΑκ÷αΫΜ”ΎΒψO'Θ§ΙΐΒψO'Ής”κx÷αΤΫ––ΒΡ÷±œΏABΘ§…δœΏO'P¥”O'A≥ωΖΔΘ§»ΤΉ≈ΒψO'Ρφ ±’κΖΫœρ–ΐΉΣ÷ΝO'BΘ§‘Ύ–ΐΉΣΒΡΙΐ≥Χ÷–Θ§Φ«ΓœAO'P=xΘ®0ΘΦxΘΦΠ–Θ©Θ§O'PΥυΨ≠ΙΐΒΡ‘ΎΒΞΈΜ‘≤OΡΎ«χ”ρΘ®“θ”Α≤ΩΖ÷Θ©ΒΡΟφΜΐΈΣSΘ°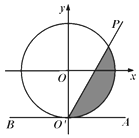
Θ®1Θ©»γΙϊ ![]() Θ§Ρ«Ο¥S=ΘΜ
Θ§Ρ«Ο¥S=ΘΜ
Θ®2Θ©ΙΊ”ΎΚ· ΐS=fΘ®xΘ©ΒΡ“‘œ¬ΝΫΗωΫα¬έΘΚ
ΔΌΕ‘»Έ“β ![]() Θ§ΕΦ”–
Θ§ΕΦ”– ![]() ΘΜ
ΘΜ
ΔΎΕ‘»Έ“βx1 Θ§ x2Γ Θ®0Θ§Π–Θ©Θ§«“x1ΓΌx2 Θ§ ΕΦ”– ![]() Θ°
Θ°
Τδ÷–’ΐ»ΖΒΡΫα¬έΒΡ–ρΚ≈ « Θ°
ΓΨ¥πΑΗΓΩ
Θ®1Θ©![]()
Θ®2Θ©ΔΌ
ΓΨΫβΈωΓΩΫβΘΚΘ®1Θ©”…Χβ“βΘ§‘≤OΒΡΑκΨΕΈΣ1Θ§»γΙϊ ![]() Θ§Ρ«Ο¥S=
Θ§Ρ«Ο¥S= ![]() Π–ΓΝ12=
Π–ΓΝ12= ![]() ΘΜΘ®2Θ©ΔΌΕ‘»Έ“β
ΘΜΘ®2Θ©ΔΌΕ‘»Έ“β ![]() Θ§ΗυΨίΆΦ–ΈΩ…ΒΟfΘ®xΘ©+fΘ®Π–©¹xΘ©Η’ΚΟΈΣΒΞΈΜ‘≤ΒΡΟφΜΐΠ–Θ§ΓΏ
Θ§ΗυΨίΆΦ–ΈΩ…ΒΟfΘ®xΘ©+fΘ®Π–©¹xΘ©Η’ΚΟΈΣΒΞΈΜ‘≤ΒΡΟφΜΐΠ–Θ§ΓΏ ![]()
![]() Θ§Ι ΔΌ’ΐ»ΖΘΜΔΎ“άΧβ“βΩ…ΒΟΚ· ΐS=fΘ®xΘ©ΒΞΒς‘ωΘ§Υυ“‘Ε‘»Έ“βx1Θ§x2Γ Θ®0Θ§Π–Θ©Θ§«“x1ΓΌx2Θ§ΕΦ”–
Θ§Ι ΔΌ’ΐ»ΖΘΜΔΎ“άΧβ“βΩ…ΒΟΚ· ΐS=fΘ®xΘ©ΒΞΒς‘ωΘ§Υυ“‘Ε‘»Έ“βx1Θ§x2Γ Θ®0Θ§Π–Θ©Θ§«“x1ΓΌx2Θ§ΕΦ”– ![]() Θ°¥μ
Θ°¥μ
Υυ“‘¥πΑΗ «ΘΚΔΌ
ΓΨΩΦΒψΨΪΈωΓΩ±ΨΧβ÷ς“ΣΩΦ≤ιΝΥ…»–ΈΟφΜΐΙΪ ΫΒΡœύΙΊ÷Σ ΕΒψΘ§–η“Σ’ΤΈ’»τ…»–ΈΒΡ‘≤–ΡΫ«ΈΣ![]() Θ§ΑκΨΕΈΣ
Θ§ΑκΨΕΈΣ![]() Θ§ΜΓ≥ΛΈΣ
Θ§ΜΓ≥ΛΈΣ![]() Θ§÷ή≥ΛΈΣ
Θ§÷ή≥ΛΈΣ![]() Θ§ΟφΜΐΈΣ
Θ§ΟφΜΐΈΣ![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§![]() Θ§
Θ§![]() ≤≈Ρή’ΐ»ΖΫβ¥π¥ΥΧβΘ°
≤≈Ρή’ΐ»ΖΫβ¥π¥ΥΧβΘ°


 ΤΏ–«ΆΦ ιΩΎΥψΥΌΥψΧλΧλΝΖœΒΝ–¥πΑΗ
ΤΏ–«ΆΦ ιΩΎΥψΥΌΥψΧλΧλΝΖœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΥΡάβΉΕP©¹ABCD÷–Θ§ADΓΈBCΘ§ADΓΆΤΫΟφPABΘ§ΓςPAB «’ΐ»ΐΫ«–ΈΘ§AD=AB=2Θ§BC=1Θ§E «œΏΕΈABΒΡ÷–Βψ 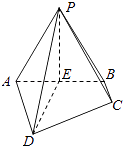
Θ®1Θ©«σ÷ΛΘΚΤΫΟφPDEΓΆΤΫΟφABCDΘΜ
Θ®2Θ©…η÷±œΏPC”κΤΫΟφPDEΥυ≥…Ϋ«ΈΣΠ»Θ§«σcosΠ»
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΦ·ΚœU={1Θ§2Θ§3Θ§4Θ§5Θ§6}Θ§A={1Θ§2Θ§3Θ§5}Θ§B={3Θ§5Θ§6}Θ°
Θ®ΔώΘ©«σAΓ…BΘΜ
Θ®ΔρΘ©«σΘ®UAΘ©Γ»BΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ ![]() ”–ΝΫΗωΝψΒψΘ°
”–ΝΫΗωΝψΒψΘ°
Θ®1Θ©»τΚ· ΐΒΡΝΫΗωΝψΒψ « ![]() ΚΆ
ΚΆ ![]() Θ§«σ
Θ§«σ ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®2Θ©»τΚ· ΐΒΡΝΫΗωΝψΒψ « ![]() ΚΆ
ΚΆ ![]() Θ§«σ
Θ§«σ ![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΥΡάβΉΕP©¹ABCD÷–ΒΉΟφΥΡ±Ώ–ΈABCD «’ΐΖΫ–ΈΘ§Ης≤ύΟφΕΦ «±Ώ≥ΛΈΣ2ΒΡ’ΐ»ΐΫ«–ΈΘ§M «άβPCΒΡ÷–ΒψΘ°Ϋ®ΝΔΩ’Φδ÷±Ϋ«Ήχ±ξœΒΘ§άϊ”ΟΩ’ΦδœρΝΩΖΫΖ®Ϋβ¥π“‘œ¬Έ ΧβΘΚ 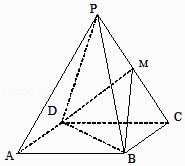
Θ®1Θ©«σ÷ΛΘΚPAΓΈΤΫΟφBMDΘΜ
Θ®2Θ©«σΕΰΟφΫ«M©¹BD©¹CΒΡΤΫΟφΫ«ΒΡ¥σ–ΓΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©Θ§Π’Θ®xΘ©¬ζΉψΙΊœΒΠ’Θ®xΘ©=fΘ®xΘ©fΘ®x+ΠΝΘ©Θ®Τδ÷–ΠΝ «≥Θ ΐΘ©Θ°
Θ®1Θ©»γΙϊΠΝ=1Θ§fΘ®xΘ©=2x©¹1Θ§«σΚ· ΐΠ’Θ®xΘ©ΒΡ÷Β”ρΘΜ
Θ®2Θ©»γΙϊΠΝ= ![]() Θ§fΘ®xΘ©=sinxΘ§«“Ε‘»Έ“βxΓ RΘ§¥φ‘Ύx1 Θ§ x2Γ RΘ§ ΙΒΟΠ’Θ®x1Θ©ΓήΠ’Θ®xΘ©ΓήΠ’Θ®x2Θ©Κψ≥…ΝΔΘ§«σ|x1©¹x2|ΒΡΉν–Γ÷ΒΘΜ
Θ§fΘ®xΘ©=sinxΘ§«“Ε‘»Έ“βxΓ RΘ§¥φ‘Ύx1 Θ§ x2Γ RΘ§ ΙΒΟΠ’Θ®x1Θ©ΓήΠ’Θ®xΘ©ΓήΠ’Θ®x2Θ©Κψ≥…ΝΔΘ§«σ|x1©¹x2|ΒΡΉν–Γ÷ΒΘΜ
Θ®3Θ©»γΙϊfΘ®xΘ©=AsinΘ®ΠΊx+Θ©Θ®AΘΨ0Θ§ΠΊΘΨ0Θ©Θ§«σΚ· ΐΠ’Θ®xΘ©ΒΡΉν–Γ’ΐ÷ήΤΎΘ®÷Μ–η–¥≥ωΫα¬έΘ©Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΫΪΚ· ΐ ![]() ΒΡΆΦœσ…œΥυ”–ΒψœρΉσΤΫ––“ΤΕ·
ΒΡΆΦœσ…œΥυ”–ΒψœρΉσΤΫ––“ΤΕ· ![]() ΗωΒΞΈΜ≥ΛΕ»Θ§ΒΟΒΫΚ· ΐgΘ®xΘ©ΒΡΆΦœσΘ§‘ρgΘ®xΘ©ΆΦœσΒΡ“ΜΧθΕ‘≥Τ÷αΒΡΖΫ≥Χ «Θ® Θ©
ΗωΒΞΈΜ≥ΛΕ»Θ§ΒΟΒΫΚ· ΐgΘ®xΘ©ΒΡΆΦœσΘ§‘ρgΘ®xΘ©ΆΦœσΒΡ“ΜΧθΕ‘≥Τ÷αΒΡΖΫ≥Χ «Θ® Θ©
A.![]()
B.![]()
C.![]()
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ![]() ΒΡΡΎΫ«
ΒΡΡΎΫ« ![]() ΒΡΕ‘±ΏΖ÷±πΈΣ
ΒΡΕ‘±ΏΖ÷±πΈΣ ![]() Θ§“―÷Σ
Θ§“―÷Σ ![]() Θ°
Θ°
Θ®ΔώΘ©«σΫ« ![]() ΒΡ¥σ–ΓΘΜ
ΒΡ¥σ–ΓΘΜ
Θ®ΔρΘ©»τ ![]() Θ§«σ
Θ§«σ ![]() ΒΡΉν¥σ÷ΒΘ°
ΒΡΉν¥σ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηf0Θ®xΘ©=sinxΘ§f1Θ®xΘ©=f0ΓδΘ®xΘ©Θ§f2Θ®xΘ©=f1ΓδΘ®xΘ©Θ§Γ≠Θ§fn+1Θ®xΘ©=fnΓδΘ®xΘ©Θ§nΓ NΘ§‘ρf2006Θ®xΘ©=Θ® Θ©
A.sinx
B.©¹sinx
C.cosx
D.©¹cosx
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com