
【题目】已知椭圆![]() 的离心率
的离心率![]() ,左右焦点分别为
,左右焦点分别为![]() 是椭圆在第一象限上的一个动点,圆
是椭圆在第一象限上的一个动点,圆![]() 与
与![]() 的延长线,
的延长线, ![]() 的延长线以及线段
的延长线以及线段![]() 都相切,
都相切, ![]() 为一个切点.
为一个切点.
(1)求椭圆方程;
(2)设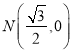 ,过
,过![]() 且不垂直于坐标轴的动点直线
且不垂直于坐标轴的动点直线![]() 交椭圆于
交椭圆于![]() 两点,若以
两点,若以![]() 为邻边的平行四边形是菱形,求直线
为邻边的平行四边形是菱形,求直线![]() 的方程.
的方程.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD及其三视图如下图所示,E是侧棱PC上的动点.
(Ⅰ)求四棱锥P﹣ABCD的体积;
(Ⅱ)不论点E在何位置,是否都有BD⊥AE?试证明你的结论;
(Ⅲ)若点E为PC的中点,求二面角D﹣AE﹣B的大小.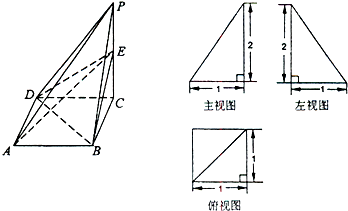
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家“十三五”计划,提出创新兴国,实现中国创新,某市教育局为了提高学生的创新能力,把行动落到实处,举办一次物理、化学综合创新技能大赛,某校对其甲、乙、丙、丁四位学生的物理成绩(x)和化学成绩(y)进行回归分析,求得回归直线方程为y=1.5x﹣35.由于某种原因,成绩表(如表所示)中缺失了乙的物理和化学成绩.
甲 | 乙 | 丙 | 丁 | |
物理成绩(x) | 75 | m | 80 | 85 |
化学成绩(y) | 80 | n | 85 | 95 |
综合素质 | 155 | 160 | 165 | 180 |
(1)请设法还原乙的物理成绩m和化学成绩n;
(2)在全市物理化学科技创新比赛中,由甲、乙、丙、丁四位学生组成学校代表队参赛.共举行3场比赛,每场比赛均由赛事主办方从学校代表中随机抽两人参赛,每场比赛所抽的选手中,只要有一名选手的综合素质分高于160分,就能为所在学校赢得一枚荣誉奖章.若记比赛中赢得荣誉奖章的枚数为ξ,试根据上表所提供数据,预测该校所获奖章数ξ的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校课改实行选修走班制,现有甲,乙,丙,丁四位学生准备选修物理,化学,生物三个科目.每位学生只选修一个科目,且选修其中任何一个科目是等可能的.
(1)恰有2人选修物理的概率;
(2)选修科目个数ξ的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,AD⊥平面BCD,CB=CD,AD=DB,P,Q分别在线段AB,AC上,AP=3PB,AQ=2QC,M是BD的中点. 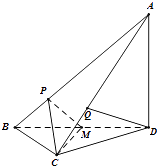
(Ⅰ)证明:DQ∥平面CPM;
(Ⅱ)若二面角C﹣AB﹣D的大小为 ![]() ,求∠BDC的正切值.
,求∠BDC的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近代统计学的发展起源于二十世纪初,它是在概率论的基础上发展起来的,统计性质的工作可以追溯到远古的“结绳记事”和《二十四史》中大量的关于我人口、钱粮、 水文、天文、地震等资料的记录.近几年,雾霾来袭,对某市该年11月份的天气情况进行统计,结果如下:表一
日期 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
天气 | 晴 | 霾 | 霾 | 阴 | 霾 | 霾 | 阴 | 霾 | 霾 | 霾 | 阴 | 晴 | 霾 | 霾 | 霾 |
日期 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
天气 | 霾 | 霾 | 霾 | 阴 | 晴 | 霾 | 霾 | 晴 | 霾 | 晴 | 霾 | 霾 | 霾 | 晴 | 霾 |
由于此种情况某市政府为减少雾霾于次年采取了全年限行的政策.
下表是一个调査机构对比以上两年11月份(该年不限行![]() 天、次年限行
天、次年限行![]() 天共
天共![]() 天)的调查结果:
天)的调查结果:
表二
不限行 | 限行 | 总计 | |
没有雾霾 |
| ||
有雾霾 |
| ||
总计 |
|
|
|
(1)请由表一数据求![]() ,并求在该年11月份任取一天,估计该市是晴天的概率;
,并求在该年11月份任取一天,估计该市是晴天的概率;
(2)请用统计学原理计算若没有![]() 的把握认为雾霾与限行有关系,则限行时有多少天没有雾霾?
的把握认为雾霾与限行有关系,则限行时有多少天没有雾霾?
(由于不能使用计算器,所以表中数据使用时四舍五入取整数)
|
|
|
|
|
|
|
|
|
|
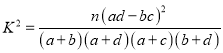
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosxsin(x+ ![]() )﹣a,且x=﹣
)﹣a,且x=﹣ ![]() 是方程f(x)=0的一个解.
是方程f(x)=0的一个解.
(1)求实数a的值及函数f(x)的最小正周期;
(2)求函数f(x)的单调递减区间;
(3)若关于x的方程f(x)=b在区间(0, ![]() )上恰有三个不相等的实数根x1 , x2 , x3 , 直接写出实数b的取值范围及x1+x2+x3的取值范围(不需要给出解题过程)
)上恰有三个不相等的实数根x1 , x2 , x3 , 直接写出实数b的取值范围及x1+x2+x3的取值范围(不需要给出解题过程)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(log2x﹣2)(log4x﹣ ![]() )
)
(1)当x∈[2,4]时,求该函数的值域;
(2)若f(x)>mlog2x对于x∈[4,16]恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O点为△ABC所在平面内一点,且满足 ![]() +2
+2 ![]() +3
+3 ![]() =
= ![]() ,现将一粒质点随机撒在△ABC内,若质点落在△AOC的概率为( )
,现将一粒质点随机撒在△ABC内,若质点落在△AOC的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com