
在对某渔业产品的质量调研中,从甲、乙两地出产的该产品中各随机抽取10件,测量该产品中某种元素的含量(单位:毫克).下表是测量数据的茎叶图: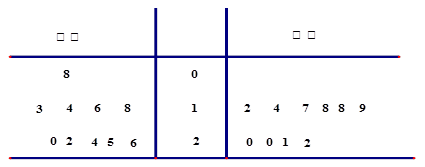
规定:当产品中的此种元素含量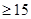 毫克时为优质品.
毫克时为优质品.
(1)试用上述样本数据估计甲、乙两地该产品的优质品率(优质品件数/总件数);
(2)从乙地抽出的上述10件产品中,随机抽取3件,求抽到的3件产品中优质品数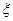 的分布列及数学期望
的分布列及数学期望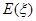 .
.
(1)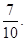 ,
, (2)
(2)
解析试题分析:(1)因为通过阅读茎叶图可得到甲、乙两组测量值的数据,又因为当产品中的此种元素含量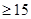 毫克时为优质品,通过数出两组优质品的数据的个数,再用优质品的的件数除以总共的样本数即可得到甲、乙的优质品率.
毫克时为优质品,通过数出两组优质品的数据的个数,再用优质品的的件数除以总共的样本数即可得到甲、乙的优质品率.
(2)因为从乙地抽出的上述10件产品中,随机抽取3件,由于乙产品中优质品有8件,所以优质品的件数共有三种情况,通过计算每种情况的概率以及数学期望的计算公式即可得到结论.
试题解析:(I)甲厂抽取的样本中优等品有7件,优等品率为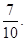
乙厂抽取的样本中优等品有8件,优等品率为
(II)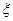 的取值为1,2,3.
的取值为1,2,3.


所以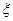 的分布列为
的分布列为
故的数学期望为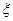
1 2 3 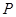


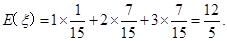
考点:1.茎叶图的知识.2.列举对比的数学思想.3.数学期望的计算.4.概率知识.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
设连续掷两次骰子得到的点数分别为m、n,令平面向量a=(m,n),b=(1,-3).
(1) 求使得事件“a⊥b”发生的概率;
(2) 求使得事件“|a|≤|b|”发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙等五名大运会志愿者被随机分到A、B、C、D四个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求甲、乙两人同时参加A岗位服务的概率;
(2)求甲、乙两人不在同一岗位服务的概率;
(3)设随机变量ξ为这五名志愿者中参加A岗位服务的人数,求ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了倡导健康、低碳、绿色的生活理念,某市建立了公共自行车服务系统鼓励市民租用公共自行车出行,公共自行车按每车每次的租用时间进行收费,具体收费标准如下:
①租用时间不超过1小时,免费;
②租用时间为1小时以上且不超过2小时,收费1元;
③租用时间为2小时以上且不超过3小时,收费2元;
④租用时间超过3小时的时段,按每小时2元收费(不足1小时的部分按1小时计算)
已知甲、乙两人独立出行,各租用公共自行车一次,两人租车时间都不会超过3小时,设甲、乙租用时间不超过1小时的概率分别是0.4和0.5;租用时间为1小时以上且不超过2小时的概率分别是0.5和0.3.
(1)求甲、乙两人所付租车费相同的概率;
(2)设甲、乙两人所付租车费之和为随机变量 ,求
,求 的分布列和数学期望E
的分布列和数学期望E .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在某城市中,M,N两地之间有整齐的方格形道路网,A1,A2,A3,A4是道路网中位于一条对角线上的4个交汇处,今在道路网M,N处的甲、乙两人分别要到N,M处,他们分别随机地选择一条沿街的最短路径,同时以每10分钟一格的速度分别向N,M处行走,直到到达N,M为止.
(1)求甲经过A2的概率.
(2)求甲、乙两人相遇经A2点的概率.
(3)求甲、乙两人相遇的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙、丙三人参加某次招聘会,假设甲能被聘用的概率是 ,甲、丙两人同时不能被聘用的概率是
,甲、丙两人同时不能被聘用的概率是 ,乙、丙两人同时能被聘用的概率为
,乙、丙两人同时能被聘用的概率为 ,且三人各自能否被聘用相互独立.
,且三人各自能否被聘用相互独立.
(1)求乙、丙两人各自被聘用的概率;
(2)设 为甲、乙、丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值,求
为甲、乙、丙三人中能被聘用的人数与不能被聘用的人数之差的绝对值,求 的分布列与均值(数学期望).
的分布列与均值(数学期望).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙两人进行投篮比赛,两人各投3球,谁投进的球数多谁获胜,已知每次投篮甲投进的概率为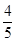 ,乙投进的概率为
,乙投进的概率为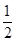 ,求:
,求:
(1)甲投进2球且乙投进1球的概率;
(2)在甲第一次投篮未投进的条件下,甲最终获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商场为吸引顾客消费推出一项促销活动,促销规则如下:到该商场购物消费满100元就可转动如图所示的转盘一次,进行抽奖(转盘为十二等分的圆盘),满200元转两次,以此类推;在转动过程中,假定指针停在转盘的任一位置都是等可能的;若转盘的指针落在A区域,则顾客中一等奖,获得10元奖金;若转盘落在B区域或C区域,则顾客中二等奖,获得5元奖金;若转盘指针落在其他区域,则不中奖(若指针停到两区间的实线处,则重新转动).若顾客在一次消费中多次中奖,则对其奖励进行累加.已知顾客甲到该商场购物消费了268元,并按照规则参与了促销活动.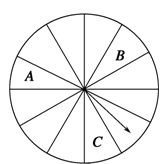
(1)求顾客甲中一等奖的概率;
(2)记X为顾客甲所得的奖金数,求X的分布列及其数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com