
【题目】函数![]() 的部分图象如图,M是图象的一个最低点,图象与x轴的一个交点的坐标为
的部分图象如图,M是图象的一个最低点,图象与x轴的一个交点的坐标为![]() ,与y轴的交点坐标为
,与y轴的交点坐标为![]() .
.
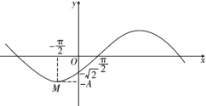
(1)求A,![]() ,
,![]() 的值;
的值;
(2)若关于x的方程![]() 在
在![]() 上有一解,求实数m的取值范围.
上有一解,求实数m的取值范围.
科目:高中数学 来源: 题型:
【题目】如图为某大河的一段支流,岸线![]() 近似满足
近似满足![]() ∥
∥![]() 宽度为7
宽度为7![]() 圆
圆![]() 为河中的一个半径为2
为河中的一个半径为2![]() 的小岛,小镇
的小岛,小镇![]() 位于岸线
位于岸线![]() 上,且满足岸线
上,且满足岸线![]() 现计划建造一条自小镇
现计划建造一条自小镇![]() 经小岛
经小岛![]() 至对岸
至对岸![]() 的通道
的通道![]() (图中粗线部分折线段,
(图中粗线部分折线段,![]() 在
在![]() 右侧),为保护小岛,
右侧),为保护小岛,![]() 段设计成与圆
段设计成与圆![]() 相切,设
相切,设![]()
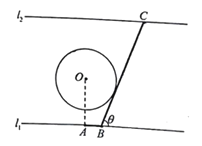
(1)试将通道![]() 的长
的长![]() 表示成
表示成![]() 的函数,并指出其定义域.
的函数,并指出其定义域.
(2)求通道![]() 的最短长.
的最短长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=2cos(2x+![]() )的图象向左平移
)的图象向左平移![]() 个单位长度,得到函数y=f(x)的图象.
个单位长度,得到函数y=f(x)的图象.
(1)求f(x)的单调递增区间;
(2)求f(x)在[0,![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年春节,各地的餐馆都出现了用餐需预定的现象,致使一些人在没有预定的情况下难以找到用餐的餐馆,针对这种现象,专家对人们的用餐地点及性别作出调查,得到的情况如下表所示:
在家用餐 | 在餐馆用餐 | 总计 | |
男性 | 30 | ||
女性 | 40 | ||
总计 | 50 | 100 |
(1)完成上述![]() 列联表;
列联表;
(2)根据表中的数据,试通过计算判断是否有![]() 的把握说明用餐地点与性别有关?
的把握说明用餐地点与性别有关?
参考公式及数据: ,其中
,其中![]() .
.
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与圆
与圆![]() 交于
交于![]() 两点,
两点,![]() 是圆
是圆![]() 上不同于
上不同于![]() 两点的动点,求
两点的动点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() x3-2x2+3x(x∈R)的图象为曲线C.
x3-2x2+3x(x∈R)的图象为曲线C.
(1)求过曲线C上任意一点切线斜率的取值范围;
(2)若在曲线C上存在两条相互垂直的切线,求其中一条切线与曲线C的切点的横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
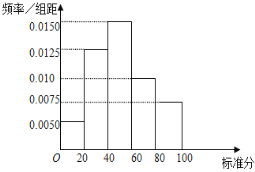
【题目】为了改善市民的生活环境,长沙某大型工业城市决定对长沙市的1万家中小型化工企业进行污染情况摸排,并出台相应的整治措施.通过对这些企业的排污口水质,周边空气质量等的检验,把污染情况综合折算成标准分100分,发现长沙市的这些化工企业污染情况标准分基本服从正态分布N(50,162),分值越低,说明污染越严重;如果分值在[50,60]内,可以认为该企业治污水平基本达标.
(Ⅰ)如图为长沙市的某工业区所有被调査的化工企业的污染情况标准分的频率分布直方图,请计算这个工业区被调査的化工企业的污染情况标准分的平均值,并判断该工业区的化工企业的治污平均值水平是否基本达标;
(Ⅱ)大量调査表明,如果污染企业继续生产,那么标准分低于18分的化工企业每月对周边造成的直接损失约为10万元,标准分在[18,34)内的化工企业每月对周边造成的直接损失约为4万元.长沙市决定关停80%的标准分低于18分的化工企业和60%的标准分在[18,34)内的化工企业,每月可减少的直接损失约有多少?
(附:若随机变量![]() ,则
,则![]() ,
, ![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com