
【题目】已知单调递增的等差数列{an},满足|a10a11|>a10a11 , 且a102<a112 , Sn为其前n项和,则( )
A.a8+a12>0
B.S1 , S2 , …S19都小于零,S10为Sn的最小值
C.a8+a13<0
D.S1 , S2 , …S20都小于零,S10为Sn的最小值
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足f(x)+f(2﹣x)=2,当x∈(0,1]时,f(x)=x2 , 当x∈(﹣1,0]时, ![]() ,若定义在(﹣1,3)上的函数g(x)=f(x)﹣t(x+1)有三个不同的零点,则实数t的取值范围是( )
,若定义在(﹣1,3)上的函数g(x)=f(x)﹣t(x+1)有三个不同的零点,则实数t的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,由三棱柱![]() 和四棱锥
和四棱锥![]() 构成的几何体中,
构成的几何体中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() .
.

(Ⅰ)求证: ![]() ;
;
(Ⅱ)若![]() 为棱
为棱![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使直线
,使直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?若存在,求
?若存在,求![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校餐厅每天供应500名学生用餐,每星期一有A、B两种菜可供选择.调查表明,凡是在这星期一选A种菜的,下星期一会有20%改选B种菜;而选B种菜的,下星期一会有30%改选A菜.用an , bn分别表示在第n个星期选A的人数和选B的人数,若a1=300,则a20=( )
A.260
B.280
C.300
D.320
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是圆
是圆![]() 上任意一点,点
上任意一点,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 分别与线段
分别与线段![]() 交于
交于![]() 两点,且
两点,且![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() 与轨迹
与轨迹![]() 相交于
相交于![]() 两点,设
两点,设![]() 为坐标原点,
为坐标原点, ![]() ,判断
,判断![]() 的面积是否为定值?若是,求出定值,若不是,说明理由.
的面积是否为定值?若是,求出定值,若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
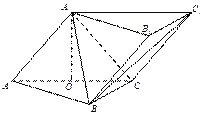
【题目】如下图,三棱柱![]() 中,侧面
中,侧面![]()
![]() 底面
底面![]() ,
, ![]() ,且
,且![]() ,O为
,O为![]() 中点.
中点.
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦;
所成角的正弦;
(Ⅲ)在![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,若不存在,说明理由;若存在,确定点
,若不存在,说明理由;若存在,确定点![]() 的位置.
的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com