
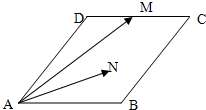
 如图,菱形ABCD的边长为2,∠A=60°,M为DC的中点,若N为菱形内任意一点(含边界),则
如图,菱形ABCD的边长为2,∠A=60°,M为DC的中点,若N为菱形内任意一点(含边界),则 的最大值为________.
的最大值为________. ,把所求问题转化为在平面区域内求线性目标函数的最值问题求解即可.
,把所求问题转化为在平面区域内求线性目标函数的最值问题求解即可.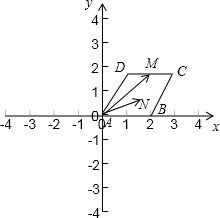
 ),D(1,
),D(1, ),M(2,
),M(2, ).
).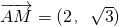 ,
, =(x,y),则
=(x,y),则 =2x+
=2x+ y,
y,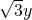 ,则
,则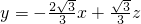 ,
, y 过点C(3,
y 过点C(3, )时,z=2x+
)时,z=2x+ y取得最大值,
y取得最大值,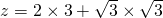 =9.
=9.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
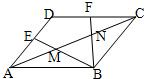 如图,菱形ABCD的边长为1,有∠D=120°,点E、F分别是AD、DC的中点,BE、BF分别与AC交于点M、N.
如图,菱形ABCD的边长为1,有∠D=120°,点E、F分别是AD、DC的中点,BE、BF分别与AC交于点M、N.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2011•西城区二模)如图,菱形ABCD的边长为6,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=3
(2011•西城区二模)如图,菱形ABCD的边长为6,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=3| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,菱形ABCD的边长为4,∠BAD=60°,AC∪BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=2
如图,菱形ABCD的边长为4,∠BAD=60°,AC∪BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=2| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=2
如图,菱形ABCD的边长为4,∠BAD=60°,AC∩BD=O.将菱形ABCD沿对角线AC折起,得到三棱锥B-ACD,点M是棱BC的中点,DM=2| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com