
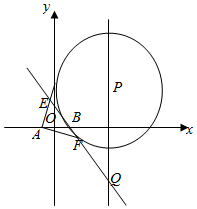
 如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(-1,0)作圆Γ的两条切线分别与l交于E,F两点.
如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(-1,0)作圆Γ的两条切线分别与l交于E,F两点.分析 (1)设AE切圆于M,直线x=4与x轴的交点为N,则EM=EB,可得|EA|+|EB|=|AM|=$\sqrt{A{P}^{2}-P{M}^{2}}$=$\sqrt{A{P}^{2}-P{B}^{2}}$=$\sqrt{A{N}^{2}-B{N}^{2}}$=4;
(2)确定E,F均在椭圆$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1上,设直线EF的方程为x=my+1(m≠0),联立,E,B,F,Q在同一条直线上,|EB|•|FQ|=|BF•|EQ|等价于-y1•$\frac{3}{m}$+y1y2=y2•$\frac{3}{m}$-y1y2,利用韦达定理,即可证明结论.
解答 证明:(1)设AE切圆于M,直线x=4与x轴的交点为N,则EM=EB,
∴|EA|+|EB|=|AM|=$\sqrt{A{P}^{2}-P{M}^{2}}$=$\sqrt{A{P}^{2}-P{B}^{2}}$=$\sqrt{A{N}^{2}-B{N}^{2}}$=4为定值;
(2)同理|FA|+|FB|=4,
∴E,F均在椭圆$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1上,
设直线EF的方程为x=my+1(m≠0),令x=4,yQ=$\frac{3}{m}$,
直线与椭圆方程联立得(3m2+4)y2+6my-9=0,
设E(x1,y1),F(x2,y2),则y1+y2=-$\frac{6m}{3{m}^{2}+4}$,y1y2=-$\frac{9}{3{m}^{2}+4}$
∵E,B,F,Q在同一条直线上,
∴|EB|•|FQ|=|BF•|EQ|等价于-y1•$\frac{3}{m}$+y1y2=y2•$\frac{3}{m}$-y1y2,
∴2y1y2=(y1+y2)•$\frac{3}{m}$,
代入y1+y2=-$\frac{6m}{3{m}^{2}+4}$,y1y2=-$\frac{9}{3{m}^{2}+4}$成立,
∴|EB|•|FQ|=|BF•|EQ|.
点评 本题考查椭圆方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=-1 | B. | y=-1 | C. | x=-2 | D. | y=-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “若a>1,则a2>1”的否命题是“若a>1,则a2≤1” | |
| B. | 在△ABC中,“A>B”是“sin2A>sin2B”必要不充分条件 | |
| C. | “若tanα$≠\sqrt{3}$,则$α≠\frac{π}{3}$”是真命题 | |
| D. | ?x0∈(-∞,0)使得3${\;}^{{x}_{0}}$<4${\;}^{{x}_{0}}$成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com