
【题目】已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的右上方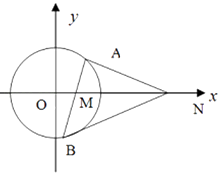
(1)求圆C的方程;
(2)过点M(1,0)的直线与圆C交于A,B两点(A在x轴上方),问在x轴正半轴上是否存在定点N,使得x轴平分∠ANB?若存在,请求出点N的坐标;若不存在,请说明理由.
【答案】
(1)解:设圆心C(a,0)(a>﹣ ![]() ),
),
∵直线l:4x+3y+10=0,半径为2的圆C与l相切,
∴d=r,即 ![]() =2,
=2,
解得:a=0或a=﹣5(舍去),
则圆C方程为x2+y2=4;
(2)解:当直线AB⊥x轴,则x轴平分∠ANB,
若x轴平分∠ANB,则kAN=﹣kBN,即 ![]() +
+ ![]() =0,
=0,
整理得:2x1x2﹣(t+1)(x1+x2)+2t=0,即 ![]() +2t=0,
+2t=0,
解得:t=4,
当点N(4,0),能使得∠ANM=∠BNM总成立.
【解析】1、根据直线与圆相切d=r可求得a=0即得结果。
2、由题意当直线AB⊥x轴,则x轴平分∠ANB,即得kAN=﹣kBN,可求出关于x的一元二次方程,利用根与系数的关系表示出两根之和与两根之积代入上式可得到t=4,即得点N(4,0)。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1、3、6、10、15、…这样的数称为“三角形数”,而把1、4、9、16、25、…这样的数称为“正方形数”.从如图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和,下列等式中,符合这一规律的是( ) 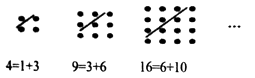
A.16=3+13
B.25=9+16
C.36=10+26
D.49=21+28
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=1,BC=2,∠CBA= ![]() ,ABEF为直角梯形,BE∥AF,∠BAF=
,ABEF为直角梯形,BE∥AF,∠BAF= ![]() ,BE=2,AF=3,平面ABCD⊥平面ABEF.
,BE=2,AF=3,平面ABCD⊥平面ABEF.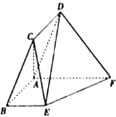
(1)求证:AC⊥平面ABEF;
(2)求平面ABCD与平面DEF所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别是△ABC的角A,B,C所对的边,且c=2,C= ![]() .
.
(1)若△ABC的面积等于 ![]() ,求a,b;
,求a,b;
(2)若sinC+sin(B﹣A)=2sin2A,求A的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=ax﹣x3(a>0,且a≠1)恰好有两个不同的零点,则实数a的取值范围是( )
A.1<a<e ![]()
B.1<a<e ![]()
C.0<a<e ![]()
D.e ![]() <a<e
<a<e ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,Sn=2n﹣an(n∈N*).
(1)计算a2 , a3 , a4 , 并由此猜想通项公式an;
(2)用数学归纳法证明(1)中的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com