【题目】用数学归纳法证明：（n+1）+（n+2）+…+（n+n）= 
（n∈N*）
【答案】证明：①n=1时，左边=2，右边=2，等式成立； ②假设n=k时，结论成立，即：（k+1）+（k+2）+…+（k+k）= 
则n=k+1时，等式左边=（k+2）+（k+3）+…+（k+k+1）+（k+1+k+1）= +3k+2= 
故n=k+1时，等式成立
由①②可知：（n+1）+（n+2）+…+（n+n）= 
（n∈N*）成立
【解析】根据数学归纳法的证题步骤，先证n=1时，等式成立；再假设n=k时，等式成立，再证n=k+1时等式成立．关键是注意n=k+1时等式左边与n=k时的等式左边的差，即为n=k+1时等式左边增加的项
【考点精析】关于本题考查的数学归纳法的定义，需要了解数学归纳法是证明关于正整数n的命题的一种方法才能得出正确答案．
科目：高中数学 来源： 题型：
【题目】双流中学校运动会招募了12名男志愿者和18名女志愿者，将这30名志愿者的身高编成如图所示的茎叶图（单位： 
)，身高在175
以上（包括175
)定义为“高个子”，身高在175
以 下（不包括175
)定义为“非高个子”.
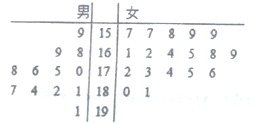
（1）如果用分层抽样的方法从“高个子”和“非高个子”中共抽取5人，再从这5人中选2人，求至少有一人是“高个子”的概率？
（2）若从身高180
以上（包括180
）的志愿者中选出男、女各一人，求这两人身高相差5
以上的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本小题满分12分）
某学校用简单随机抽样方法抽取了100名同学，对其日均课外阅读时间（单位：分钟）进行调查，结果如下：
t |
|
|
|
|
|
|
男同学人数 | 7 | 11 | 15 | 12 | 2 | 1 |
女同学人数 | 8 | 9 | 17 | 13 | 3 | 2 |
若将日均课外阅读时间不低于60分钟的学生称为“读书迷”.
（1）将频率视为概率，估计该校4000名学生中“读书迷”有多少人？
（2）从已抽取的8名“读书迷”中随机抽取4位同学参加读书日宣传活动.
（i）求抽取的4位同学中既有男同学又有女同学的概率；
（ii）记抽取的“读书迷”中男生人数为
，求
的分布列和数学期望
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=|2x﹣1|+|2x+a|，g（x）=x+3． （Ⅰ）当a=﹣2时，求不等式f（x）＜g（x）的解集；
（Ⅱ）设a＞﹣1，且当 
时，f（x）≤g（x），求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知命题p：设a，b∈R，则“a+b＞4”是“a＞2且b＞2”的必要不充分条件；命题q：若 
＜0，则 
， 
夹角为钝角，在命题①p∧q；②￢p∨￢q；③p∨￢q；④￢p∨q中，真命题是（ ）
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
对任意实数
恒有
，且当
时， 
，又
.
(1)判断
的奇偶性；
(2)求证： 
是R上的减函数；
(3)求
在区间[－3,3]上的值域；
(4)若x∈R，不等式
恒成立，求实数
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在棱长为2的正方体ABCD﹣A1B1C1D1中，E，F分别为A1B1 ， CD的中点．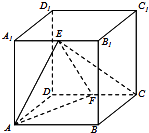 
（1）求| 
|
（2）求直线EC与AF所成角的余弦值；
（3）求二面角E﹣AF﹣B的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，设椭圆
： 
的离心率为
， 
分别为椭圆
的左、右顶点， 
为右焦点，直线
与
的交点到
轴的距离为
，过点
作
轴的垂线
， 
为
上异于点
的一点，以
为直径作圆
.
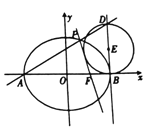
（1）求
的方程；
（2）若直线
与
的另一个交点为
，证明：直线
与圆
相切.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（本题满分12分）已知函数f(x)＝2cos x(sin x＋cos x)．
(1)求f
的值；
(2)求函数f(x)的最小正周期及单调递增区间．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
