
在△ABC中,角A,B,C的对边分别为a,b,c,且c=2,C=60°.
(1)求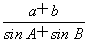 的值;
的值;
(2)若a+b=ab,求△ABC的面积.
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷3练习卷(解析版) 题型:选择题
设等差数列{an}的前n项和为Sn,若Sm-1=-2,Sm=0,Sm+1=3,则m=( )
A.3 B.4 C.5 D.6
查看答案和解析>>
科目:高中数学 来源:2013-2014学年(安徽专用)高考数学(文)专题阶段评估模拟卷1练习卷(解析版) 题型:选择题
设z=x+y,其中实数x,y满足 若z的最大值为6,则z的最小值为( )
若z的最大值为6,则z的最小值为( )
A.-3 B.-2
C.-1 D.0
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练解答题押题练C组练习卷(解析版) 题型:解答题
已知向量m=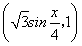 ,n=
,n=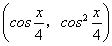 .
.
(1)若m·n=1,求cos 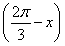 的值;
的值;
(2)记f(x)=m·n,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cos B=bcos C,求函数f(A)的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练解答题押题练A组练习卷(解析版) 题型:解答题
已知函数f(x)=x2+2ax+1(a∈R),f′(x)是f(x)的导函数.
(1)若x∈[-2,-1],不等式f(x)≤f′(x)恒成立,求a的取值范围;
(2)解关于x的方程f(x)=|f′(x)|; ?
(3)设函数g(x)=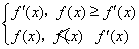 ,求g(x)在x∈[2,4]时的最小值.
,求g(x)在x∈[2,4]时的最小值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练填空题押题练F组练习卷(解析版) 题型:填空题
设l是一条直线,α,β,γ是不同的平面,则在下列命题中,假命题是________.
①如果α⊥β,那么α内一定存在直线平行于β
②如果α不垂直于β,那么α内一定不存在直线垂直于β
③如果α⊥γ,β⊥γ,α∩β=l,那么l⊥γ
④如果α⊥β,l与α,β都相交,那么l与α,β所成的角互余
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练填空题押题练F组练习卷(解析版) 题型:填空题
为了分析某篮球运动员在比赛中发挥的稳定程度,统计了该运动员在6场比赛中的得分,用茎叶图表示如图所示,则该组数据的方差为________.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学(文)三轮专题体系通关训练填空题押题练D组练习卷(解析版) 题型:填空题
已知函数f(x)=-xln x+ax在(0,e)上是增函数,函数g(x)=|ex-a|+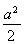 ,当x∈[0,ln 3]时,函数g(x)的最大值M与最小值m的差为
,当x∈[0,ln 3]时,函数g(x)的最大值M与最小值m的差为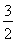 ,则a=________.
,则a=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com