
对于函数 ![]() ,若存在
,若存在![]() ,使
,使 ![]() 成立,则称
成立,则称![]() 为
为![]() 的“滞点”.已知函数f ( x ) =
的“滞点”.已知函数f ( x ) = ![]() .
.
(I)试问![]() 有无“滞点”?若有,求之,否则说明理由;
有无“滞点”?若有,求之,否则说明理由;
(II)已知数列![]() 的各项均为负数,且满足
的各项均为负数,且满足![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(III)已知![]() ,求
,求![]() 的前项和
的前项和![]() .
.
科目:高中数学 来源: 题型:
对于函数![]() ,若存在
,若存在![]() 成立,则称
成立,则称![]() 的不动点。如果函数
的不动点。如果函数![]() 有且只有两个不动点0,2,且
有且只有两个不动点0,2,且![]()
(1)求函数![]() 的解析式;
的解析式;
(2)已知各项不为零的数列![]() ,求数列通项
,求数列通项![]() ;
;
(3)如果数列![]() 满足
满足![]() ,求证:当
,求证:当![]() 时,恒有
时,恒有![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源:2011届河南省卫辉市第一中学高三一月月考数学理卷 题型:解答题
(本小题满分12分)
对于函数 ,若存在
,若存在 R,使
R,使 成立,则称
成立,则称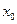 为
为 的不动点.如果函数
的不动点.如果函数 N*
N* 有且仅有两个不动点0和2,且
有且仅有两个不动点0和2,且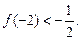
(1)求实数 ,
, 的值;
的值;
(2)已知各项不为零的数列
 ,并且
,并且 , 求数列
, 求数列 的通项公式;;
的通项公式;;
(3)求证: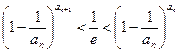 .
.
查看答案和解析>>
科目:高中数学 来源:2013届海南省高二下学期期末考试文科数学试卷(解析版) 题型:解答题
对于函数 ,若存在实数
,若存在实数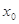 ,使
,使 成立,则称
成立,则称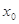 为
为 的不动点.
的不动点.
⑴当 时,求
时,求 的不动点;
的不动点;
⑵若对于任何实数 ,函数
,函数 恒有两相异的不动点,求实数
恒有两相异的不动点,求实数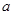 的取值范围;
的取值范围;
⑶在⑵的条件下,若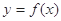 的图象上A、B两点的横坐标是函数
的图象上A、B两点的横坐标是函数 的不动点,且直线
的不动点,且直线 是线段AB的垂直平分线,求实数b的取值范围.
是线段AB的垂直平分线,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆市高三12月月考理科数学卷 题型:解答题
(本小题满分12分)
对于函数 ,若存在
,若存在 R,使
R,使 成立,则称
成立,则称 为
为 的不动点.如果函数
的不动点.如果函数 N*
N* 有且仅有两个不动点0和2,且
有且仅有两个不动点0和2,且
(1)求实数 ,
, 的值;
的值;
(2)已知各项不为零的数列
 ,并且
,并且 , 求数列
, 求数列 的通项公式;;
的通项公式;;
(3)求证: .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com