
分析 作辅助图象,设直线l的方程为y=kx+m(k<0),从而联立化简可得(3+4k2)x2+8kmx+4m2-12=0,从而可得点P(-$\frac{4k}{\sqrt{3+4{k}^{2}}}$,$\frac{3}{\sqrt{4{k}^{2}+3}}$),写出直线l1的方程为x+ky=0,从而得到d=$\frac{1}{\sqrt{4{k}^{2}+\frac{3}{{k}^{2}}+7}}$,从而确定利用基本不等式确定最大值即可.
解答 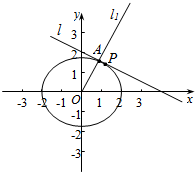 解:作辅助图象如右图,
解:作辅助图象如右图,
设直线l的方程为y=kx+m(k<0),
由$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$消y得,
(3+4k2)x2+8kmx+4m2-12=0,
∵直线l与椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1只有一个公共点P,
∴△=(8km)2-4(3+4k2)(4m2-12)=0,
即m2-4k2-3=0,即m=$\sqrt{4{k}^{2}+3}$,
故点P(-$\frac{4k}{\sqrt{3+4{k}^{2}}}$,$\frac{3}{\sqrt{4{k}^{2}+3}}$),
∵直线l1过原点且与l垂直,
∴直线l1的方程为x+ky=0,
∴P点到直线l1的距离d=$\frac{|-\frac{4k}{\sqrt{4{k}^{2}+3}}+\frac{3k}{\sqrt{4{k}^{2}+3}}|}{\sqrt{1+{k}^{2}}}$
=$\frac{1}{\sqrt{4{k}^{2}+\frac{3}{{k}^{2}}+7}}$,
∵4k2+$\frac{3}{{k}^{2}}$≥2$\sqrt{12}$=4$\sqrt{3}$,
(当且仅当4k2=$\frac{3}{{k}^{2}}$时,等号成立);
∴4k2+$\frac{3}{{k}^{2}}$+7≥7+4$\sqrt{3}$=(2+$\sqrt{3}$)2,
故$\frac{1}{\sqrt{4{k}^{2}+\frac{3}{{k}^{2}}+7}}$≤2-$\sqrt{3}$;
故P点到直线l1的距离的最大值为2-$\sqrt{3}$;
故答案为:2-$\sqrt{3}$.
点评 本题考查了数形结合的思想应用及椭圆与直线的关系应用,同时考查了基本不等式的应用及化简运算能力.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:选择题
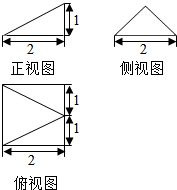
| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com