
| 树干周长(单位:cm) | [30,40) | [40,50) | [50,60) | [60,70) |
| 杉树 | 6 | 19 | 21 | x |
| 槐树 | 4 | 20 | y | 6 |
分析 (1)因为按分层抽样方法随机抽取100株,可得槐树为40,杉树60株,由此能求出x,y值.
(2)根据已知条件列举法得到基本事件数为12种,而设事件A:排查的树木恰好为2株,事件A包含基本事件个数为3种,可用公式解得所求概率.
解答 解:(1)按分层抽样方法随机抽取100株,可得槐树为40,杉树60株
∴x=60-6-19-21=14,y=40-4-20-6=10.
(2)设4株树为B1、B2、B3、D,设D为有虫害的那株,
基本事件为:(B1,B2)、(B1,B3)、(B1,D)、(B2,B1)、(B2,B3)、(B2,D)、
(B3,B1)、(B3,B2)、(B3,D)、(D,B1)、(D,B2)、(D,B3),共12种,
设事件A:排查的树木恰好为2株,事件A包含(B1,D)、(B2,D)、(B3,D)3种,
∴P(A)=$\frac{3}{12}$=$\frac{1}{4}$.
点评 本题考查分层抽样的应用,考查概率的求法,是基础题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{{4\sqrt{5}}}{5}$ | C. | $\frac{{2\sqrt{3}}}{3}$ | D. | $\frac{{4\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,$\frac{1}{2}$] | B. | (-2,$\frac{1}{2}$] | C. | [-2,$\frac{1}{2}$) | D. | (-2,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
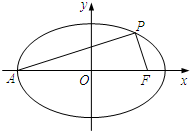 如图,在平面直角坐标系xOy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,右焦点为F(c,0),P(x0,y0)为椭圆上一点,且PA⊥PF.
如图,在平面直角坐标系xOy中,椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,右焦点为F(c,0),P(x0,y0)为椭圆上一点,且PA⊥PF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com