
| A. | 过抛物线x2=-2py焦点的直线被抛物线截得的最短弦长为2p | |
| B. | 命题“有些自然数是偶数”是特称命题 | |
| C. | 离心率为$\sqrt{2}$的双曲线的两渐近线互相垂直 | |
| D. | 对于空间向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,则有($\overrightarrow{a}$•$\overrightarrow{b}$)$\overrightarrow{c}$=$\overrightarrow{a}$($\overrightarrow{b}$•$\overrightarrow{c}$) |
分析 根据抛物线的简单性质,特称命题的概念,双曲线的简单性质,数乘向量的几何意义,分别判断四个命题的真假,可得答案.
解答 解:过抛物线x2=-2py焦点的直线与抛物线的对称轴垂直时,被抛物线截得的最短,此时弦长为2p,故A是真命题;
命题“有些自然数是偶数”是特称命题,故B是真命题;
离心率为$\sqrt{2}$的双曲线方程为:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{a}^{2}}=1$,渐近线为y=±x,互相垂直,故C是真命题;
对于空间向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$表示与$\overrightarrow{c}$平行的向量,$\overrightarrow{a}$•($\overrightarrow{b}$•$\overrightarrow{c}$)表示与$\overrightarrow{a}$平行的向量,但$\overrightarrow{a}$与$\overrightarrow{c}$不一定平行,故D为假命题,
故选:D
点评 本题考查的知识点是命题的真假判断与应用,抛物线的简单性质,特称命题的概念,双曲线的简单性质,数乘向量的几何意义,难度中档.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | {a,c,d,e} | B. | {a,c} | C. | {b,d} | D. | {d} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
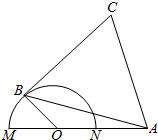 如图半⊙O的直径为2,A为直径MN延长线上一点,且OA=2,B为半圆周上任一点,以AB为边作等边△ABC(A、B、C按顺时针方向排列)问∠AOB为多少时,四边形OACB的面积最大?这个最大面积是多少?
如图半⊙O的直径为2,A为直径MN延长线上一点,且OA=2,B为半圆周上任一点,以AB为边作等边△ABC(A、B、C按顺时针方向排列)问∠AOB为多少时,四边形OACB的面积最大?这个最大面积是多少?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{12}{13}$ | B. | $\frac{5}{13}$ | C. | -$\frac{5}{13}$ | D. | -$\frac{12}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | 3 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com