
分析 (1)根据已知条件,得出b=c,由圆的直径得出2a.进而得基本参数a,b,c.
(2)直线与圆位置关系,构造直角三角形用勾股关系求得|MN|,直线与椭圆采用设而不求法,根据韦达定理求得弦长|AB|,都转化为关于斜率k的函数求取值范围.
解答 解:(Ⅰ)因为椭圆C长轴长等于圆R:x2+(y-2)2=4的直径,
所以2a=4,a=2;又2b=2c,
所以$b=c=\sqrt{2}$,
所以椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$;…(3分)
(Ⅱ)当直线l的斜率不存在时,|AB|=2$\sqrt{2}$,|MN|=4,|AB|•|MN|=8$\sqrt{2}$;…(4分)
当直线l的斜率存在时,设l的方程为y=kx+1,与$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$联立,
消去y,得(1+2k2)x2+4kx-2=0;
由△>0,可得k∈R…(5分)
设A(x1,y1),B(x2,y2),
则x1+x2=$-\frac{4k}{1+2{k}^{2}}$,x1x2=$-\frac{2}{1+2{k}^{2}}$,
|AB|=$\sqrt{1+{k}^{2}}$•|x1-x2|=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$
=$\sqrt{1+{k}^{2}}$•$\sqrt{(-\frac{4k}{1+2{k}^{2}})^{2}+\frac{8}{1+2{k}^{2}}}$
=$\sqrt{1+{k}^{2}}$•$\frac{\sqrt{32{k}^{2}+8}}{1+2{k}^{2}}$,…(7分)
|MN|=2$\sqrt{4-(\frac{1}{\sqrt{1+{k}^{2}}})^{2}}$=2$\sqrt{\frac{4{k}^{2}+3}{1+{k}^{2}}}$,…(9分)
所以|AB|•|MN|=$\sqrt{1+{k}^{2}}$•$\frac{\sqrt{32{k}^{2}+8}}{1+2{k}^{2}}$•2$\sqrt{\frac{4{k}^{2}+3}{1+{k}^{2}}}$
=4$\sqrt{2}$•$\frac{\sqrt{4{k}^{2}+1}•\sqrt{4{k}^{2}+3}}{1+2{k}^{2}}$
=$4\sqrt{2}\sqrt{4-\frac{1}{{{{(1+2{k^2})}^2}}}}∈[4\sqrt{6},8\sqrt{2})$
综上,|AB|•|MN|的取值范围是[4$\sqrt{6}$,8$\sqrt{2}$].…12
点评 考查了求椭圆标准方程,直线与圆、椭圆的位置关系.考查了设而不求法,函数思想.化简及求范围有一定难度,故属于难题;易忽略斜率不存在这类,故属于易错题.


科目:高中数学 来源: 题型:选择题
| A. | 2a-1 | B. | 2-a-1 | C. | 1-2-a | D. | 1-2a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
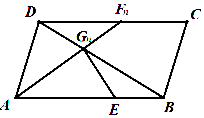 如图,已知点E为平行四边形ABCD的边AB上一点,$\overrightarrow{AE}$=2$\overrightarrow{EB}$,Fn(n∈N*)为边DC上的一列点,连接AFn交BD于Gn,点Gn(n∈N*)满足$\overrightarrow{{G_n}D}$=$\frac{1}{3}$an+1$\overrightarrow{{G_n}A}$-(3an+2)$\overrightarrow{{G_n}E}$,其中数列{an}是首项为1的正项数列,则a4的值为( )
如图,已知点E为平行四边形ABCD的边AB上一点,$\overrightarrow{AE}$=2$\overrightarrow{EB}$,Fn(n∈N*)为边DC上的一列点,连接AFn交BD于Gn,点Gn(n∈N*)满足$\overrightarrow{{G_n}D}$=$\frac{1}{3}$an+1$\overrightarrow{{G_n}A}$-(3an+2)$\overrightarrow{{G_n}E}$,其中数列{an}是首项为1的正项数列,则a4的值为( )| A. | 45 | B. | 51 | C. | 53 | D. | 61 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,五面体ABCDFE中,AB∥CD∥EF,四边形ABCD,ABEF,CDFE都是等腰梯形,并且平面ABCD⊥平面ABEF,AB=12,CD=3,EF=4,梯形ABCD的高为3,EF到平面ABCD的距离为6,则此五面体的体积为57.
如图所示,五面体ABCDFE中,AB∥CD∥EF,四边形ABCD,ABEF,CDFE都是等腰梯形,并且平面ABCD⊥平面ABEF,AB=12,CD=3,EF=4,梯形ABCD的高为3,EF到平面ABCD的距离为6,则此五面体的体积为57.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com