
已知函数f(x)=(x-1)2,g(x)=4(x-1),数列{an}是各项均不为0的等差数列,其前n项和为Sn,点(an+1,S2n-1)在函数f(x)的图象上;数列{bn}满足b1=2,bn≠1,且(bn-bn+1)·g(bn)=f(bn)(n∈N+).
(1)求an并证明数列{bn-1}是等比数列;
(2)若数列{cn}满足cn= ,证明:c1+c2+c3+…+cn<3.
,证明:c1+c2+c3+…+cn<3.
(1)an=2n-1.,见解析(2)见解析
【解析】(1)因为点(an+1,S2n-1)在函数f(x)的图象上,所以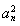 =S2n-1.
=S2n-1.
令n=1,n=2,得 即
即 解得a1=1,d=2(d=-1舍去),则an=2n-1.
解得a1=1,d=2(d=-1舍去),则an=2n-1.
由(bn-bn+1)·g(bn)=f(bn),
得4(bn-bn+1)(bn-1)=(bn-1)2.
由题意bn≠1,所以4(bn-bn+1)=bn-1,
即3(bn-1)=4(bn+1-1),所以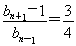 .
.
所以数列{bn-1}是以1为首项,公比为 的等比数列.
的等比数列.
(2由(1),得bn-1= n-1.
n-1.
cn= =
= =
= .
.
令Tn=c1+c2+c3+…+cn,
则Tn=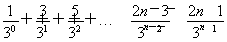 ,①
,①
 Tn=
Tn= ,②
,②
①-②得, Tn=
Tn= +
+ +
+ +
+ +…+
+…+ -
- =1+
=1+ -
- =2-
=2- -
- =2-
=2- .所以Tn=3-
.所以Tn=3- .
.
所以c1+c2+c3+…+cn=3- <3.
<3.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用19练习卷(解析版) 题型:解答题
设M是把坐标平面上的点的横坐标伸长到2倍,纵坐标伸长到3倍的伸压变换.
(1)求矩阵M的特征值及相应的特征向量;
(2)求逆矩阵M-1以及椭圆 =1在M-1的作用下的新曲线的方程.
=1在M-1的作用下的新曲线的方程.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用13练习卷(解析版) 题型:填空题
在平面直角坐标系xOy中,以椭圆 =1(a>b>0)上的一点A为圆心的圆与x轴相切于椭圆的一个焦点,与y轴相交于B、C两点,若△ABC是锐角三角形,则该椭圆的离心率的取值范围是________.
=1(a>b>0)上的一点A为圆心的圆与x轴相切于椭圆的一个焦点,与y轴相交于B、C两点,若△ABC是锐角三角形,则该椭圆的离心率的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用11练习卷(解析版) 题型:解答题
已知双曲线x2- =1.
=1.

(1)若一椭圆与该双曲线共焦点,且有一交点P(2,3),求椭圆方程.
(2)设(1)中椭圆的左、右顶点分别为A、B,右焦点为F,直线l为椭圆的右准线,N为l上的一动点,且在x轴上方,直线AN与椭圆交于点M.若AM=MN,求∠AMB的余弦值;
(3)设过A、F、N三点的圆与y轴交于P、Q两点,当线段PQ的中点为(0,9)时,求这个圆的方程.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用11练习卷(解析版) 题型:填空题
已知圆的方程为x2+y2-6x-8y=0,设该圆中过点(3,5)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用10练习卷(解析版) 题型:填空题
已知首项为正数的等差数列{an}的前n项和为Sn,若a1 006和a1 007是方程x2-2 012x-2 011=0的两根,则使Sn>0成立的正整数n的最大值是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试选择填空限时训练4练习卷(解析版) 题型:填空题
已知一个正方体的所有顶点在一个球面上.若球的体积为 π,则正方体的棱长为________.
π,则正方体的棱长为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试选择填空限时训练3练习卷(解析版) 题型:填空题
已知正方形ABCD的边长为2, E为CD的中点,则 ·
· =________.
=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试选择填空限时训练1练习卷(解析版) 题型:选择题
已知四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,PA=PD=2,平面PAD⊥平面ABCD,则它的正视图的面积为( )

A. B.
B.  C.
C.  D.3
D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com