[题目]点S.A.B.C在半径为的同一球面上.点S到平面ABC的距离为 .AB=BC=CA= .则点S与△ABC中心的距离为( )A.B.C.1D. 题目和参考答案——青夏教育精英家教网—

【题目】点S、A、B、C在半径为的同一球面上，点S到平面ABC的距离为，AB=BC=CA= ，则点S与△ABC中心的距离为（）
A.
B.
C.1
D.

【答案】B
【解析】解：如图，∵点S、A、B、C在半径为的同一球面上，点S到平面ABC的距离为，AB=BC=CA= ，
设△ABC的外接圆的圆心为M，过S作SD⊥平面ABC，交MC于D，
连结OD，OS，过S作MO的垂线SE，交MO于点E，
∴半径r=MC= =1，∴MO= = =1，
∵SD⊥MC，ME⊥MC，∴MESD是矩形，∴ME=SD= ，
∴MD=SE= = = ，
∴SM= = = ．
故选：B．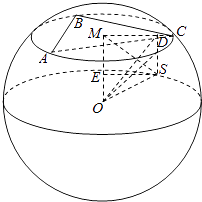

设△ABC的外接圆的圆心为M，协S作SD⊥平面ABC，交MC于D，连结OD，OS，过S作MO的垂线SE，交MO于点E，由题意求出MC=MO=1，从而得到ME=SD= ，进而求出MD=SE= ，由此能求出点S与△ABC中心的距离．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知定义在R上的奇函数f（x）满足f（x）=x2﹣2x﹣3（x＞0）．
（Ⅰ）若函数g（x）=|f（x）|﹣a有4个零点，求实数a的取值范围；
（Ⅱ）求|f（x+1）|≤4的解集．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图所示，已知四棱锥P—ABCD，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°,E,F分别是BC,PC的中点.

(1)证明:AE⊥PD;

(2)若H为PD上的动点,EH与平面PAD所成最大角的正切值为,

求二面角E—AF—C的余弦值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，四棱锥中，底面为平行四边形.底面 .

（I）证明：

（II）设，求棱锥的高.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图四面体ABCD中，△ABC是正三角形，AD=CD．（12分）
（1）证明：AC⊥BD；
（2）已知△ACD是直角三角形，AB=BD，若E为棱BD上与D不重合的点，且AE⊥EC，求四面体ABCE与四面体ACDE的体积比．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】根据某水文观测点的历史统计数据，得到某河流水位X（单位：米）的频率分布直方图如图：将河流水位在以上6段的频率作为相应段的概率，并假设每年河流水位互不影响．
（1）求未来三年，至多有1年河流水位X∈[27，31）的概率（结果用分数表示）；
（2）该河流对沿河A企业影响如下：当X∈[23，27）时，不会造成影响；当X∈[27，31）时，损失10000元；当X∈[31，35）时，损失60000元，为减少损失，现有种应对方案：方案一：防御35米的最高水位，需要工程费用3800元；
方案二：防御不超过31米的水位，需要工程费用2000元；
方案三：不采取措施；
试比较哪种方案较好，并请说理由．