
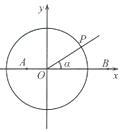
 如图,在平面直角坐标系中,点A(-$\frac{1}{2}$,0),B($\frac{3}{2}$,0),锐角α的终边与单位圆O交于点P.
如图,在平面直角坐标系中,点A(-$\frac{1}{2}$,0),B($\frac{3}{2}$,0),锐角α的终边与单位圆O交于点P.分析 (Ⅰ)用α的三角函数的坐标法定义得到P 坐标;
(Ⅱ)首先写成两个向量的坐标根据$\overrightarrow{AP}$•$\overrightarrow{BP}$=-$\frac{1}{4}$,得到关于α的三角函数等式,求α的值;
(Ⅲ)假设存在M(x,0),进行向量的模长运算,得到三角等式,求得成立的x值.
解答 解:锐角α的终边与单位圆O交于点P.
(Ⅰ)用α的三角函数表示点P的坐标为(cosα,sinα);
(Ⅱ)$\overrightarrow{AP}=(cosα+\frac{1}{2},sinα)$,$\overrightarrow{BP}=(cosα-\frac{3}{2},sinα)$,$\overrightarrow{AP}$•$\overrightarrow{BP}$=-$\frac{1}{4}$时,
即(cos$α+\frac{1}{2}$)(cos$α-\frac{3}{2}$)+sin2α=$\frac{-1}{4}$,整理得到cos$α=\frac{1}{2}$,所以锐角α=60°;
(Ⅲ)在x轴上假设存在定点M,设M(x,0),$\overrightarrow{MP}=(cosα-x,sinα)$,
则由|$\overrightarrow{AP}$|=$\frac{1}{2}$|$\overrightarrow{MP}$|恒成立,得到$\frac{5}{4}+cosα$=$\frac{1}{4}(1-2xcosα+{x}^{2})$,整理得2cosα(2+x)=x2-4,
所以存在x=-2时等式恒成立,所以存在M(-2,0).
点评 本题考查了三角函数的坐标法定义的运用以及平面向量的运算;关键是正确利用坐标表示各向量,并正确化简运算.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | -$\frac{4}{3}$ | D. | ±$\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -9 | B. | -1 | C. | 1 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>0且m≠1 | B. | m≠$\frac{1}{3}$ | C. | m>$\frac{1}{3}$且m≠$\frac{2}{3}$ | D. | $\frac{1}{3}$<m<$\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com