
【题目】已知函数f(x)=ex﹣mx,
(1)求函数f(x)的单调区间.
(2)若函数g(x)=f(x)﹣lnx+x2存在两个零点,求m的取值范围.
【答案】
(1)解:f′(x)=ex﹣m,
若m≤0,则f′(x)>0恒成立,
f(x)在R递增,无递减区间;
m>0时,由f′(x)=0,得:x=lnm,
令f′(x)>0,解得:x>lnm,
令f′(x)<0,解得:x<lnm,
故f(x)在(﹣∞,lnm)递减,在(lnm,+∞)递增
(2)解:由g(x)=f(x)﹣lnx+x2=0,
得m= ![]() ,
,
令h(x)= ![]() ,
,
则h′(x)= ![]() ,
,
观察得x=1时,h′(x)=0.
当x>1时,h′(x)>0,
当0<x<1时,h′(x)<0,
∴h(x)min=h(1)=e+1,
∴函数g(x)=f(x)﹣lnx+x2存在两个零点时,m的取值范围是(e+1,+∞)
【解析】(1)求出函数的导数,通过讨论m的范围,求出函数的单调区间即可;(2)由g(x)=f(x)﹣lnx+x2=0,分离出m,令h(x)= ![]() ,由此能求出函数g(x)=f(x)﹣lnx+x2存在两个零点时m的取值范围.
,由此能求出函数g(x)=f(x)﹣lnx+x2存在两个零点时m的取值范围.
【考点精析】利用利用导数研究函数的单调性对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.


科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(2x﹣ ![]() )的图象,可以将函数y=sin2x的图象( )
)的图象,可以将函数y=sin2x的图象( )
A.向右平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向左平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O1和圆O2的极坐标方程分别为ρ=2, ![]() .
.
(1)把圆O1和圆O2的极坐标方程化为直角坐标方程;
(2)求经过两圆交点的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《最强大脑》是大型科学竞技类真人秀节目,是专注传播脑科学知识和脑力竞技的节目.某机构为了了解大学生喜欢《最强大脑》是否与性别有关,对某校的100名大学生进行了问卷调查,得到如下列联表:
喜欢《最强大脑》 | 不喜欢《最强大脑》 | 合计 | |
男生 | 15 | ||
女生 | 15 | ||
合计 |
已知在这100人中随机抽取1人抽到不喜欢《最强大脑》的大学生的概率为0.4
( I)请将上述列联表补充完整;判断是否有99.9%的把握认为喜欢《最强大脑》与性别有关,并说明理由;
( II)已知在被调查的大学生中有5名是大一学生,其中3名喜欢《最强大脑》,现从这5名大一学生中随机抽取2人,抽到喜欢《最强大脑》的人数为X,求X的分布列及数学期望.
下面的临界值表仅参考:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2=![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数f(x)是定义在(﹣2,2)上的减函数,则不等式f( ![]() )+f(2x﹣1)>0的解集是( )
)+f(2x﹣1)>0的解集是( )
A.(﹣∞, ![]() )
)
B.[﹣ ![]() ,+∞)
,+∞)
C.(﹣6,﹣ ![]() )
)
D.(﹣ ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ),x∈R(其中 ![]() )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为 ![]() ,且图象上一个最低点为
,且图象上一个最低点为 ![]() . (Ⅰ)求f(x)的解析式;
. (Ⅰ)求f(x)的解析式;
(Ⅱ)当 ![]() ,求f(x)的值域.
,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直线l1:kx+y=0和直线l2:kx+y+b=0(b>0),射线OC的一个法向量为 ![]() =(﹣k,1),点O为坐标原点,且k≥0,直线l1和l2之间的距离为2,点A、B分别是直线l1、l2上的动点,P(4,2),PM⊥l1于点M,PN⊥OC于点N;
=(﹣k,1),点O为坐标原点,且k≥0,直线l1和l2之间的距离为2,点A、B分别是直线l1、l2上的动点,P(4,2),PM⊥l1于点M,PN⊥OC于点N; 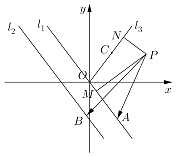
(1)若k=1,求|OM|+|ON|的值;
(2)若| ![]() |=8,求
|=8,求 ![]() 的最大值;
的最大值;
(3)若k=0,AB⊥l2 , 且Q(﹣4,﹣4),试求|PA|+|AB|+|BQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理中是演绎推理的序号为( )
A.由金、银、铜、铁可导电,猜想:金属都可导电
B.猜想数列 ![]() {an}的通项公式为
{an}的通项公式为 ![]() (n∈N+)
(n∈N+)
C.半径为r圆的面积S=πr2 , 则单位圆的面积S=π
D.由平面直角坐标系中圆的方程为(x﹣a)2+(y﹣b)2=r2 , 推测空间直角坐标系中球的方程为(x﹣a)2+(y﹣b)2+(z﹣c)2=r2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com