
【题目】在平面直角坐标系中,曲线C的参数方程为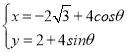 (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为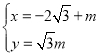 (m为参数),以平面直角坐标系的原点O为极点,x轴正半轴为极轴,建立坐标系.
(m为参数),以平面直角坐标系的原点O为极点,x轴正半轴为极轴,建立坐标系.
(1)求曲线C的极坐标方程;
(2)直线l与曲线C相交于M,N两点,若![]() ,求
,求![]() 的值.
的值.
 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】动点![]() 在椭圆
在椭圆![]() 上,过点
上,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 满足
满足![]() ,已知点
,已知点![]() 的轨迹是过点
的轨迹是过点![]() 的圆.
的圆.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 在
在![]() 轴的同侧),
轴的同侧),![]() ,
,![]() 为椭圆的左、右焦点,若
为椭圆的左、右焦点,若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
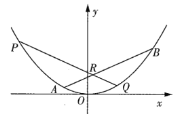
【题目】如图,斜率为![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,已知点
两点,已知点![]() 的横坐标比点
的横坐标比点![]() 的横坐标大4,直线
的横坐标大4,直线![]() 交线段
交线段![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() .
.
(1)若点![]() 的横坐标等于0,求
的横坐标等于0,求![]() 的值;
的值;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建极坐标系,直线
轴的非负半轴为极轴建极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(Ⅰ)求![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)射线![]() 与圆C的交点为
与圆C的交点为![]() 与直线
与直线![]() 的交点为
的交点为![]() ,求
,求![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下列两个命题,命题甲:平面α与平面β相交;命题乙:相交直线l,m都在平面α内,并且都不在平面β内,直线l,m中至少有一条与平面β相交.则甲是乙的( )
A.充分且必要条件B.充分而不必要条件
C.必要而不充分条件D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的各项均为正数,其前n项的积为
的各项均为正数,其前n项的积为![]() ,记
,记![]() ,
,![]() .
.
(1)若数列![]() 为等比数列,数列
为等比数列,数列![]() 为等差数列,求数列
为等差数列,求数列![]() 的公比.
的公比.
(2)若![]() ,
,![]() ,且
,且![]()
①求数列![]() 的通项公式.
的通项公式.
②记![]() ,那么数列
,那么数列![]() 中是否存在两项
中是否存在两项![]() ,(s,t均为正偶数,且
,(s,t均为正偶数,且![]() ),使得数列
),使得数列![]() ,
,![]() ,
,![]() ,成等差数列?若存在,求s,t的值;若不存在,请说明理由.
,成等差数列?若存在,求s,t的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了提升学生“数学建模”的核心素养,某校数学兴趣活动小组指导老师给学生布置了一项探究任务:如图,有一张边长为27cm的等边三角形纸片ABC,从中裁出等边三角形纸片![]() 作为底面,从剩余梯形
作为底面,从剩余梯形![]() 中裁出三个全等的矩形作为侧面,围成一个无盖的三棱柱(不计损耗).
中裁出三个全等的矩形作为侧面,围成一个无盖的三棱柱(不计损耗).
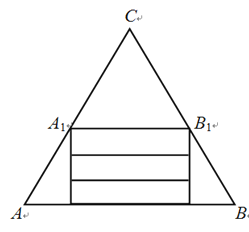
(1)若三棱柱的侧面积等于底面积,求此三棱柱的底面边长;
(2)当三棱柱的底面边长为何值时,三棱柱的体积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机的普及,手机计步软件迅速流行开来,这类软件能自动记载每个人每日健步的步数,从而为科学健身提供一定的帮助.某市工会为了解该市市民每日健步走的情况,从本市市民中随机抽取了2000名市民(其中不超过40岁的市民恰好有1000名),利用手机计步软件统计了他们某天健步的步数,并将样本数据分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 九组(单位:千步),将抽取的不超过40岁的市民的样本数据绘制成频率分布直方图如右,将40岁以上的市民的样本数据绘制成频数分布表如下,并利用该样本的频率分布估计总体的概率分布.
九组(单位:千步),将抽取的不超过40岁的市民的样本数据绘制成频率分布直方图如右,将40岁以上的市民的样本数据绘制成频数分布表如下,并利用该样本的频率分布估计总体的概率分布.
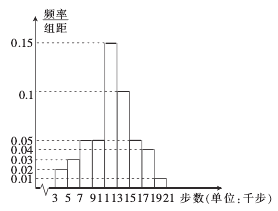
分组 (单位:千步) |
|
|
|
|
|
|
|
|
|
频数 | 10 | 20 | 20 | 30 | 400 | 200 | 200 | 100 | 20 |
(1)现规定,日健步步数不低于13000步的为“健步达人”,填写下面列联表,并根据列联表判断能否有![]() %的把握认为是否为“健步达人”与年龄有关;
%的把握认为是否为“健步达人”与年龄有关;
健步达人 | 非健步达人 | 总计 | |
40岁以上的市民 | |||
不超过40岁的市民 | |||
总计 |
(2)(ⅰ)利用样本平均数和中位数估计该市不超过40岁的市民日健步步数(单位:千步)的平均数和中位数;
(ⅱ)由频率分布直方图可以认为,不超过40岁的市民日健步步数![]() (单位:千步)近似地服从正态分布
(单位:千步)近似地服从正态分布![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() (每组数据取区间的中点值),
(每组数据取区间的中点值),![]() 的值已求出约为
的值已求出约为![]() .现从该市不超过40岁的市民中随机抽取5人,记其中日健步步数
.现从该市不超过40岁的市民中随机抽取5人,记其中日健步步数![]() 位于
位于![]() 的人数为
的人数为![]() ,求
,求![]() 的数学期望.
的数学期望.
参考公式: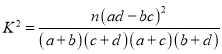 ,其中
,其中![]() .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com