
【题目】设抛物线y2=4x的焦点为F,准线为l.已知点C在l上,以C为圆心的圆与y轴的正半轴相切于点A.若∠FAC=120°,则圆的方
程为 .
科目:高中数学 来源: 题型:
【题目】如图,椭圆 ![]() =1(a>b>0)的左、右顶点分别为A,B,焦距为2
=1(a>b>0)的左、右顶点分别为A,B,焦距为2 ![]() ,直线x=﹣a与y=b交于点D,且|BD|=3
,直线x=﹣a与y=b交于点D,且|BD|=3 ![]() ,过点B作直线l交直线x=﹣a于点M,交椭圆于另一点P.
,过点B作直线l交直线x=﹣a于点M,交椭圆于另一点P. 
(1)求椭圆的方程;
(2)证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一次考试成绩的样本频率分布直方图(样本容量n=200),若成绩不低于60分为及格,则样本中的及格人数是( )
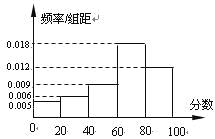
A. 6 B. 36 C. 60 D. 120
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图4所示,其中成绩分组区间是: ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
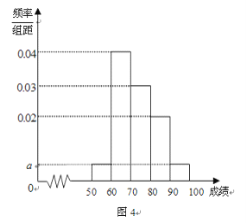
(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数![]() 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数![]() 之比如下表所示,求数学成绩在
之比如下表所示,求数学成绩在![]() 之外的人数.
之外的人数.
分数段 |
|
|
|
|
X:y | 1:1 | 2:1 | 3:4 | 4:5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表数据是水的温度x(℃)对黄酮延长性y(%)效应的试验结果,y是以延长度计算的.
x/℃ | 300 | 400 | 500 | 600 | 700 | 800 |
y/% | 40 | 50 | 55 | 60 | 67 | 70 |
(1)画出散点图;
(2)指出x,y是否线性相关,若线性相关,求y关于x的回归方程;
(3)估计水的温度是1000 ℃时,黄酮延长性的情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌豆腐食品是经过A,B,C三道工序加工而成的,A,B,C工序的产品合格率分别为![]() ,
,![]() ,
,![]() .已知每道工序的加工都相互独立,三道工序加工的产品都合格时产品为一等品;恰有两次合格为二等品;其他的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工的产品都合格时产品为一等品;恰有两次合格为二等品;其他的为废品,不进入市场.
(1)生产一袋豆腐食品,求产品为废品的概率;
(2)生产一袋豆腐食品,设X为三道加工工序中产品合格的工序数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x3﹣ ![]() x2+6x+m.
x2+6x+m.
(1)对于x∈R,f′(x)≥a恒成立,求a的最大值;
(2)若方程f(x)=0有且仅有一个实根,求m的取值范围;
(3)当m=2时,若函数g(x)= ![]() +
+ ![]() x﹣6+2blnx(b≠0)在[1,2]上单调递减,求实数b的最大值.
x﹣6+2blnx(b≠0)在[1,2]上单调递减,求实数b的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com