
【题目】已知函数![]() 且
且![]() 是
是![]() 的导函数,则过曲线
的导函数,则过曲线![]() 上一点
上一点![]() 的切线方程为
的切线方程为![]()
![]()
A. ![]() B.
B. ![]()
C. ![]() 或
或![]() D.
D. ![]() 或
或![]()
【答案】A
【解析】
先根据a=f′(![]() )求出a的值,再根据题意求出b的值和切线的斜率,再写出切线的方程.
)求出a的值,再根据题意求出b的值和切线的斜率,再写出切线的方程.
(1)由f(x)=3x+cos2x+sin2x
得f′(x)=3-2sin2x+2cos2x,
则a=f′(![]() )=3-2sin
)=3-2sin![]() +2cos
+2cos![]() =1.
=1.
由y=x3得y′=3x2,
当P点为切点时,切线的斜率k=3a2=3×12=3.
又b=a3,则b=1,所以切点P的坐标为(1,1).
故过曲线y=x3上的点P的切线方程为y-1=3(x-1),
即3x-y-2=0.
当P点不是切点时,设切点为(x0,x),
∴切线方程为y-x=3x (x-x0),
∵P(a,b)在曲线y=x3上,且a=1,∴b=1.
∴1-x=3x (1-x0),
∴2x-3x+1=0,∴2x-2x-x+1=0,
∴(x0-1)2(2x0+1)=0,∴切点为![]() ,
,
∴此时的切线方程为y+![]() =
=![]()
![]() ,
,
综上,满足题意的切线方程为3x-y-2=0或3x-4y+1=0,
故答案为:C


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图1,在正方形![]() 中,
中,![]() 是
是![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,且
上,且![]() .若将
.若将![]() 分别沿
分别沿![]() 折起,使
折起,使![]() 两点重合于点
两点重合于点![]() ,如图2.
,如图2.
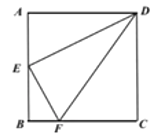
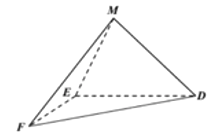
图1 图2
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】轮船A从某港口O要将一些物品送到正航行的轮船B上,在轮船A出发时,轮船B位于港口O北偏西30°且与O相距20海里的P处,并正以15海里/时的航速沿正东方向匀速行驶,假设轮船A沿直线方向以v海里/时的航速匀速行驶,经过t小时与轮船B相遇,
(1)若使相遇时轮船A航距最短,则轮船A的航行速度的大小应为多少?
(2)假设轮船B的航行速度为30海里/时,轮船A的最高航速只能达到30海里/时,则轮船A以多大速度及沿什么航行方向行驶才能在最短时间内与轮船B相遇,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是R上的奇函数,且x>0时,f(x)=x2-4x+3.
求:(1)f(x)的解析式.
(2)已知t>0,求函数f(x)在区间[t,t+1]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以![]() 为首项的数列
为首项的数列![]() 满足:
满足:![]() .
.
(1)当![]() 时,且
时,且![]() ,写出
,写出![]() 、
、![]() ;
;
(2)若数列![]() 是公差为-1的等差数列,求
是公差为-1的等差数列,求![]() 的取值范围;
的取值范围;
(3)记![]() 为
为![]() 的前
的前![]() 项和,当
项和,当![]() 时,
时,
①给定常数![]() ,求
,求![]() 的最小值;
的最小值;
②对于数列![]() ,
,![]() ,…,
,…,![]() ,当
,当![]() 取到最小值时,是否唯一存在满足
取到最小值时,是否唯一存在满足![]() 的数列
的数列![]() ?说明理由.
?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】江苏省淮阴中学科技兴趣小组在计算机上模拟航天器变轨返回试验.设计方案如图,航天器运行(按顺时针方向)的轨迹方程为![]() ,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以
,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以![]() 轴为对称轴、
轴为对称轴、![]() 为顶点的抛物线的实线部分,降落点为
为顶点的抛物线的实线部分,降落点为![]() .观测点
.观测点![]() 同时跟踪航天器,试问:当航天器在
同时跟踪航天器,试问:当航天器在![]() 轴上方时,观测点
轴上方时,观测点![]() ,
,![]() 测得离航天器的距离分别为多少时,应向航天器发出变轨指令?(变轨指令发出时航天器立即变轨)。
测得离航天器的距离分别为多少时,应向航天器发出变轨指令?(变轨指令发出时航天器立即变轨)。

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】狄利克雷函数是高等数学中的一个典型函数,若![]() ,则称
,则称![]() 为狄利克雷函数.对于狄利克雷函数
为狄利克雷函数.对于狄利克雷函数![]() ,给出下面4个命题:①对任意
,给出下面4个命题:①对任意![]() ,都有
,都有![]() ;②对任意
;②对任意![]() ,都有
,都有![]() ;③对任意
;③对任意![]() ,都有
,都有![]() ,
, ![]() ;④对任意
;④对任意![]() ,都有
,都有![]() .其中所有真命题的序号是( )
.其中所有真命题的序号是( )
A. ①④ B. ②③ C. ①②③ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD和矩形ABEF中,![]() ,
,![]() ,矩形ABEF可沿AB任意翻折.
,矩形ABEF可沿AB任意翻折.
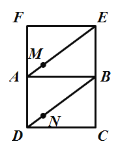
(1)求证:当点F,A,D不共线时,线段MN总平行于平面ADF.
(2)“不管怎样翻折矩形ABEF,线段MN总与线段FD平行”这个结论正确吗?如果正确,请证明;如果不正确,请说明能否改变个别已知条件使上述结论成立,并给出理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某便利店计划每天购进某品牌鲜奶若干件,便利店每销售一瓶鲜奶可获利![]() 元;若供大于求,剩余鲜奶全部退回,但每瓶鲜奶亏损
元;若供大于求,剩余鲜奶全部退回,但每瓶鲜奶亏损![]() 元;若供不应求,则便利店可从外调剂,此时每瓶调剂品可获利
元;若供不应求,则便利店可从外调剂,此时每瓶调剂品可获利![]() 元.
元.
(1)若便利店一天购进鲜奶![]() 瓶,求当天的利润
瓶,求当天的利润![]() (单位:元)关于当天鲜奶需求量
(单位:元)关于当天鲜奶需求量![]() (单位:瓶,
(单位:瓶,![]() )的函数解析式;
)的函数解析式;
(2)便利店记录了![]() 天该鲜奶的日需求量
天该鲜奶的日需求量![]() (单位:瓶,
(单位:瓶,![]() )整理得下表:
)整理得下表:
日需求量 |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
若便利店一天购进![]() 瓶该鲜奶,以
瓶该鲜奶,以![]() 天记录的各需求量的频率作为各需求量发生的概率,求当天利润在区间
天记录的各需求量的频率作为各需求量发生的概率,求当天利润在区间![]() 内的概率.
内的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com