
【题目】已知集合![]() ,集合
,集合![]() ,
,![]() ,
,![]() 满足.
满足.
①每个集合都恰有5个元素
②![]()
![]()
![]()
集合![]() 中元素的最大值与最小值之和称为集合
中元素的最大值与最小值之和称为集合![]() 的特征数,记为
的特征数,记为![]() ,则
,则![]()
![]()
![]() 的值不可能为( )
的值不可能为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】分析:求出集合M={x∈N*|1≤x≤15}={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15},由题意列举出集合A1,A2,A3,排除选项B、C、D,由此能求出结果.
详解:由题意集合M={x∈N*|1≤x≤15}={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15},
当A1={1,4,5,6,7},A2={3,12,13,14,15},A3={2,8,9,10,11}时,
X1+X2+X3=8+18+13=39,故排除B选项;
当A1={1,4,5,6,15},A2={2,7,8,9,14},A3={3,10,11,12,13}时,
X1+X2+X3=16+16+16=48,故排除C选项;
当A1={1,2,3,4,15},A2={5,6,7,8,14},A3={9,10,11,12,13}时,
X1+X2+X3=16+19+22=57,故排除D选项.
∴X1+X2+X3的值不可能为37.
故选A.


科目:高中数学 来源: 题型:
【题目】某工厂采用甲、乙两种不同生产方式生产某零件,现对两种生产方式所生产的这种零件的产品质量进行对比,其质量按测试指标可划分为:指标在区间![]() 100的为一等品;指标在区间
100的为一等品;指标在区间![]() 的为二等品
的为二等品![]() 现分别从甲、乙两种不同生产方式所生产的零件中,各自随机抽取100件作为样本进行检测,测试指标结果的频率分布直方图如图所示:
现分别从甲、乙两种不同生产方式所生产的零件中,各自随机抽取100件作为样本进行检测,测试指标结果的频率分布直方图如图所示:
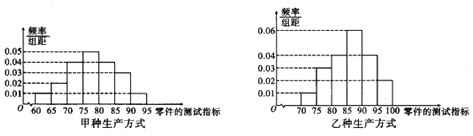
![]() 若在甲种生产方式生产的这100件零件中按等级,利用分层抽样的方法抽取10件,再从这10件零件中随机抽取3件,求至少有1件一等品的概率;
若在甲种生产方式生产的这100件零件中按等级,利用分层抽样的方法抽取10件,再从这10件零件中随机抽取3件,求至少有1件一等品的概率;
![]() 将频率分布直方图中的频率视作概率,用样本估计总体
将频率分布直方图中的频率视作概率,用样本估计总体![]() 若从该厂采用乙种生产方式所生产的所有这种零件中随机抽取3件,记3件零件中所含一等品的件数为X,求X的分布列及数学期望.
若从该厂采用乙种生产方式所生产的所有这种零件中随机抽取3件,记3件零件中所含一等品的件数为X,求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,圆心为坐标原点的单位圆O在C的内部,且与C有且仅有两个公共点,直线
,圆心为坐标原点的单位圆O在C的内部,且与C有且仅有两个公共点,直线![]() 与C只有一个公共点.
与C只有一个公共点.
(1)求C的标准方程;
(2)设不垂直于坐标轴的动直线l过椭圆C的左焦点F,直线l与C交于A,B两点,且弦AB的中垂线交x轴于点P,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解公司800名员工对公司食堂组建的需求程度,将这些员工编号为1,2,3,…,800,对这些员工使用系统抽样的方法等距抽取100人征求意见,有下述三个结论:①若25号员工被抽到,则105号员工也会被抽到;②若32号员工被抽到,则1到100号的员工中被抽取了10人;③若88号员工未被抽到,则10号员工一定未被抽到;其中正确的结论个数为( )
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com