下列命题中:
①f(x)的图象与f(-x)关于y轴对称.
②f(x)的图象与-f(-x)的图象关于原点对称.
③y=|lgx|与y=lg|x|的定义域相同,它们都只有一个零点.
④二次函数f(x)满足f(2-x)=f(2+x)并且有最小值,则f(0)<f(5).
⑤若定义在R上的奇函数f(x),有f(3+x)=-f(x),则f(2010)=0
其中所有正确命题的序号是 .
【答案】
分析:①②可以根据偶函数和奇函数的定义进行证明;
③根据对数函数的性质以及绝对值的性质进行求解;
④可以根据f(2-x)=f(2+x),求出其对称轴,有最小值,开口向上,利用图象进行求解;
⑤根据在R上的奇函数f(x),有f(3+x)=-f(x),求出其周期后进行判断;
解答:解:①f(x)的图象与f(-x),对任意的(a,f(a))在f(x)的图象上,可得关于y轴对称的点(-a,f(a))在f(-x)的图象上,故①正确;
②f(x)的图象与-f(-x)的图象,对任意的(a,f(a))在f(x)的图象上,可得关于原点对称的点(-a,-f(a))在-f(-x)的图象上,故②正确;
③y=|lgx|可得定义域为:{x|x>0},y=lg|x|的定义域为{x|x≠0},故③错误;
④二次函数f(x)满足f(2-x)=f(2+x),对称轴为x=
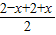
=2,f(x)有最小值,故函数开口向上,可知f(0)=f(4),f(x)在(2,+∞)上为增函数,∴f(0)=f(4)<f(5),故④正确;
⑤定义在R上的奇函数f(x),可得f(0)=0,
∵有f(3+x)=-f(x),可得f(x+3)=-f(x+6),可得f(x)=f(x+6),其周期为T=6,
∴f(2010)=f(335×6)=f(0)=0,故⑤正确;
故答案为①②④⑤;
点评:此题主要考查命题的真假命题的判定及其应用,考查了对数函数的性质以及奇函数的性质,是一道基础题;

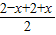 =2,f(x)有最小值,故函数开口向上,可知f(0)=f(4),f(x)在(2,+∞)上为增函数,∴f(0)=f(4)<f(5),故④正确;
=2,f(x)有最小值,故函数开口向上,可知f(0)=f(4),f(x)在(2,+∞)上为增函数,∴f(0)=f(4)<f(5),故④正确;

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案