
| 使用年数x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 年均价格 y(美元) | 2 651 | 1 943 | 1 494 | 1 087 | 765 | 538 | 484 | 290 | 226 | 204 |
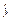 =e-0.298x+8.165
=e-0.298x+8.165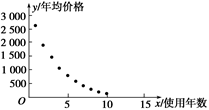
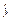 =e
=e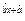 来刻画题中模型更为合理,令
来刻画题中模型更为合理,令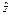 =ln
=ln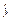 ,则
,则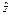 =
=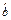 x+
x+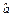 ,题中数据变成如下表所示:
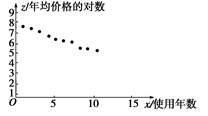
,题中数据变成如下表所示:| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| z | 7.883 | 7.572 | 7.309 | 6.991 | 6.640 | 6.288 | 6.182 | 5.670 | 5.421 | 5.318 |
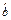 ≈-0.298,
≈-0.298,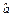 ≈8.165,所以
≈8.165,所以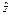 =-0.298x+8.165,最后回代
=-0.298x+8.165,最后回代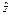 =ln
=ln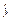 ,即
,即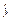 =e-0.298x+8.165为所求.
=e-0.298x+8.165为所求.

科目:高中数学 来源:不详 题型:单选题
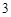 岁至
岁至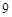 岁的身高,数据如下表,由此建立的身高与年龄的回归模型为
岁的身高,数据如下表,由此建立的身高与年龄的回归模型为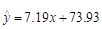 .用这个模型预测这个孩子
.用这个模型预测这个孩子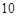 岁时的身高,则正确的叙述是
岁时的身高,则正确的叙述是 | 年龄/岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
身高/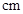 | 94.8 | 104.2 | 108.7 | 117.8 | 124.3 | 130.8 | 139.0 |
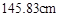 B.身高在
B.身高在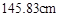 以上
以上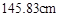 左右 D.身高在
左右 D.身高在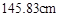 以下
以下查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 性别 性别药 恢复效果 | 男运动员 | 女运动员 | ||
| 未用 | 用 | 未用 | 用 | |
| 有效(恢复得好) 无效(恢复得差) | 60 45 | 120 45 | 45 60 | 180 |
| 255 | ||||
| 总 计 | 105 | 165 | 105 | 435 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
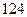 人,其中六十岁以上的
人,其中六十岁以上的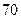 人,六十岁以下的
人,六十岁以下的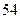 人,六十岁以上的人中有
人,六十岁以上的人中有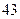 人的饮食以蔬菜为主,另外
人的饮食以蔬菜为主,另外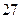 人则以肉类为主;六十岁以下的人中有
人则以肉类为主;六十岁以下的人中有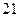 人饮食以蔬菜为主,另外
人饮食以蔬菜为主,另外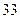 人则以肉类为主.(1)根据以上数据建立一个
人则以肉类为主.(1)根据以上数据建立一个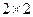 的列联表;(2)判断人的饮食习惯是否与年龄有关.
的列联表;(2)判断人的饮食习惯是否与年龄有关.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 号电池
号电池 节,
节, 号电池
号电池 节,总质量为
节,总质量为 ;第二天收集
;第二天收集 号电池
号电池 节,
节, 号电池
号电池 节,总质量为
节,总质量为 .
. 号电池和
号电池和 号电池每节质量各为多少克?
号电池每节质量各为多少克? 天收
天收 号废电池(单位:节) 号废电池(单位:节) |  |  |  |  |  |
 号废电池(单位:节) 号废电池(单位:节) |  | 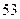 |  |  |  |
 天两种废电池每天平均收集多少节?并由此估计四月份环保小组收集废电池的总质量是多少千克?
天两种废电池每天平均收集多少节?并由此估计四月份环保小组收集废电池的总质量是多少千克?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
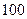 位居民进行调查,经过计算
位居民进行调查,经过计算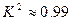 ,根据这一数据分析,下列说法正确的是 ( )
,根据这一数据分析,下列说法正确的是 ( )A.有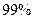 的人认为该栏目优秀 的人认为该栏目优秀 |
B.有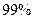 的人认为该栏目是否优秀与改革有关系 的人认为该栏目是否优秀与改革有关系 |
C.有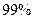 的把握认为电视栏目是否优秀与改革有关系 的把握认为电视栏目是否优秀与改革有关系 |
| D.没有理由认为电视栏目是否优秀与改革有关系 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 患心脏病 | 未患心脏病 | 合计 |
| 每一晚都打鼾 | 30 | 224 | 254 |
| 不打鼾 | 24 | 1355 | 1379 |
| 合计 | 54 | 1579 | 1633 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
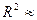 。
。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com