
(2)设a,b,c为一个不等边三角形的三边,求证:abc>(b+c-a)(a+b-c)(c+a-b).
(3)已知a>0,b>0,a+b=1,求证:(1+![]() )(1+
)(1+![]() )≥25.
)≥25.
(4)设x>0,y>0,求证:![]() .
.
证明:(1)∵a>0,b>0,c>0且a+b+c=1,
∴1-a=b+c>0.
同理,1-b=a+c>0,1-c=a+b>0,
∴(1-a)(1-b)(1-c)=(a+b)(b+c)(a+c).∵a+b≥2![]() >0,b+c≥2
>0,b+c≥2![]() >0,a+c≥2
>0,a+c≥2![]() >0,
>0,
∴(a+b)(b+c)(a+c)≥2![]() ·2
·2![]() ·2
·2![]() =8abc(当a=b=c=
=8abc(当a=b=c=![]() 时,等号成立).
时,等号成立).
(2)∵a,b,c为一个不等边三角形的三边,
∴a>0,b>0,c>0且a+b-c>0,a+c-b>0,b+c-a>0.
∵a=![]() ≥
≥![]() >0,
>0,
同理,b=![]() ≥
≥![]() >0,
>0,
c=![]() >0,
>0,
由于三角形是不等边三角形,上述三式不能同时取“=”,
∴abc>(a+b-c)(b+c-a)(c+a-b).
(3)设y=![]() =
=![]() =
=![]()
∵a>0,b>0,a+b=1,
∴a2+2ab+b2=1.
∴a2+b2=1-2ab.
∴y=1+![]() 令t=
令t=![]() ,则y=2t2-2t+1.
,则y=2t2-2t+1.
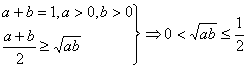 ,即0<ab≤
,即0<ab≤![]() .
.
∴![]() ≥4,即t∈[4,+∞).
≥4,即t∈[4,+∞).
由二次函数的性质可知对称轴t=![]() .
.
y=2t2-2t+1在t∈[4,+∞)上是增函数.
∴当t=4时,y取最小值25.故(1+![]() )(1+
)(1+![]() )≥25.
)≥25.
(4)∵x>0,y>0,∴(x2+y2)3=x6+y6+3x2y2(x2+y2)≥x6+y6+6x3y3>x6+y6+2x3y3=(x3+y3)2.
由不等式的性质,两边同时开6次方,得![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
A.k2-e2>1 B.k2-e2<1
C.e2-k2>1 D.e2-k2<1
查看答案和解析>>
科目:高中数学 来源: 题型:
函数f(x)在定义域R内可导,若f(x)=f(2-x),且当x∈(-∞,1)时,(x-1)![]() <0,设a=f(0),b= f(
<0,设a=f(0),b= f(![]() ),c= f(3),则 ( )
),c= f(3),则 ( )
A .a<b<c B.c<a<b C.c<b<a D.b<c<a
查看答案和解析>>
科目:高中数学 来源:2013届内蒙古巴彦淖尔市高二第一学期期中考试数学 题型:解答题
(1)设a > 0 ,
b > 0 , 求证:  a
+ b ;
a
+ b ;
(2)设x,y都是正实数 ,且x + y = 1 ,求证:(1+
 )(1+
)(1+
 )
≥ 9 .
)
≥ 9 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com