Question

18．已知点A（4，0），抛物线C：x²=8y的焦点为F，射线FA与抛物线和它的准线分别交于点M和N，则|FM|：|MN|=1：$\sqrt{5}$．

Answer 1

分析 如图所示，由抛物线定义知|MF|=|MH|，得到|FM|：|MN|=|MH|：|MN|，根据△MHN∽△FOA，即可求出答案．

解答 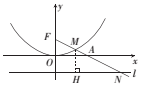解：如图所示，由抛物线定义知|MF|=|MH|，
所以|FM|：|MN|=|MH|：|MN|．
由于△MHN∽△FOA，
则$\frac{|MH|}{|HN|}$=$\frac{|OF|}{|OA|}$=$\frac{2}{4}$=$\frac{1}{2}$，
则|MH|：|MN|=1：$\sqrt{5}$，
即|FM|：|MN|=1：$\sqrt{5}$．
故答案为：1：$\sqrt{5}$

点评 本题给出抛物线方程和射线FA，求线段的比值、抛物线的定义、标准方程和简单几何性质等知识，属于中档题．