
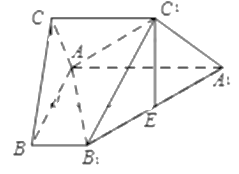
【题目】多面体![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 在平面
在平面![]() 上的射影
上的射影![]() 是线段
是线段![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】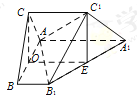
试题分析:(1)过E作EO//A1A交AB于O,连接CO,先证明四边形OEC1C是平行四边形,可得C1E//CO,由C1E⊥面ABB1A1,得CO⊥面ABB1A1,进而可得结论;(2)以点O为坐标原点以![]() 为轴建立空间直角坐标系,分别求出平面AB1C1的法向量与平面A1B1BA的法向量,利用空间向量夹角余弦公式可得结果.
为轴建立空间直角坐标系,分别求出平面AB1C1的法向量与平面A1B1BA的法向量,利用空间向量夹角余弦公式可得结果.
试题解析:(1)证明:过E作EO//A1A交AB于O,连接CO,
由梯形的中位线知: ![]() ,
,
∴OE=CC1,又OE//CC1,
故四边形OEC1C是平行四边形,
∴C1E⊥面ABB1A1,则CO⊥面ABB1A1,
又CO在面ABC内,
∴面ABC⊥面ABB1A1;

(2)如图以点O为坐标原点建立空间直角坐标系, CO=C1E=2, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
设面AB1C1的法向量为![]() ,
,
依题知: 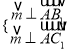 ,即
,即![]() ,
,
令a=1,得b=-2,c=2,∴![]() ,底面A1B1BA的法向量为
,底面A1B1BA的法向量为![]() ,
,
∴![]() .
.
∴二面角C1-AB1-A1的余弦值为![]() .
.
【方法点晴】本题主要考查线面垂直、面面垂直的判定,利用空间向量求二面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系(5)根据定理结论求出相应的角和距离.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:高中数学 来源: 题型:
【题目】设f(x)是偶函数,且在(0,+∞)内是减函数,又f(﹣3)=0,则xf(x)>0的解集是( )
A.{x|﹣3<x<0或x>3}
B.{x|x<﹣3或x>3}
C.{x|﹣3<x<0或x<x<3}
D.{x|x<﹣3或0<x<3}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为 ![]() (α为参数),在以原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为
(α为参数),在以原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为 ![]() .
.
(1)求C的普通方程和l的倾斜角;
(2)设点P(0,2),l和C交于A,B两点,求|PA|+|PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学得到方程2x+e﹣0.3x﹣100=0(其中e=2.7182…)的大于零的近似解依次为①50;②50.1;③49.5;④50.001,你认为的答案为最佳近似解(请填甲、乙、丙、丁中的一个)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)当a>0时,求函数f(x)的单调递减区间;
(Ⅱ)当a=0时,设函数g(x)=xf(x)﹣k(x+2)+2.若函数g(x)在区间![]() 上有两个零点,求实数k的取值范围.
上有两个零点,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合,极轴与![]() 轴的正半轴重合,圆
轴的正半轴重合,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为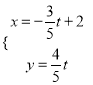 (
(![]() 为参数).
为参数).
(Ⅰ)若![]() ,
, ![]() 是直线
是直线![]() 与
与![]() 轴的交点,
轴的交点, ![]() 是圆
是圆![]() 上一动点,求
上一动点,求![]() 的最大值;
的最大值;
(Ⅱ)若直线![]() 被圆
被圆![]() 截得的弦长等于圆
截得的弦长等于圆![]() 的半径
的半径![]() 倍,求
倍,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x),g(x)分别是R上的奇函数、偶函数,且满足f(x)﹣g(x)=ex , 则有( )
A.f(2)<f(3)<g(0)
B.g(0)<f(3)<f(2)
C.f(2)<g(0)<f(3)
D.g(0)<f(2)<f(3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点![]() ,点
,点![]() ,
, ![]() 是椭圆上异于长轴端点的两个点.
是椭圆上异于长轴端点的两个点.
(1)求椭圆![]() 的离心率;
的离心率;
(2)已知直线![]() :
: ![]() ,且
,且![]() ,垂足为
,垂足为![]() ,
, ![]() ,垂足为
,垂足为![]() ,若
,若![]() 且
且![]() ,求
,求![]() 中点的轨迹方程.
中点的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com