
(1)a取什么值时,C1和C2有且仅有一条公切线?写出此公切线的方程.
(2)若C1和C2有两条公切线,证明相应的两条公切线段互相平分.
(1)解:函数y=x2+2x的导数y′=2x+2,曲线C1在点P(x1,x21+2x1)的切线方程是y-(x21+2x1)=(2x1+2)(x-x1),即y=(2x1+2)x-x21. ①
函数y=-x2+a的导数y′=-2x,曲线C2在点Q(x2,-x22+a)的切线方程是y-(-x22+a)=-2x2(x-x2),即y=-2x2x+x22+a. ②
如果直线l是过P和Q的公切线,则①式和②式都是l的方程![]() 消去x2得方程2x21+2x1+1+a=0,此方程Δ=4-4×2(1+a).
消去x2得方程2x21+2x1+1+a=0,此方程Δ=4-4×2(1+a).
由Δ=0,得a=-![]() ,解得x1=-
,解得x1=-![]() ,此时P与Q重合,即当a=-
,此时P与Q重合,即当a=-![]() 时,C1和C2有且仅有一条公切线.
时,C1和C2有且仅有一条公切线.
由①得公切线方程为y=x-![]() .
.
(2)证明:由(1)可知,当a<-![]() 时,C1和C2有两条公切线,设一条公切线上切点为P(x1,y1)、Q(x2,y2),其中P在C1上,Q在C2上,则有x1+x2=-1,y1+y2=x21+2x1+(-x22+a)=x21+2x1-(x1+1)2+a=-1+a,线段PQ的中点为(
时,C1和C2有两条公切线,设一条公切线上切点为P(x1,y1)、Q(x2,y2),其中P在C1上,Q在C2上,则有x1+x2=-1,y1+y2=x21+2x1+(-x22+a)=x21+2x1-(x1+1)2+a=-1+a,线段PQ的中点为(![]() ).
).
同理,另一条公切线段P′Q′的中点也是(![]() ),
),
所以公切线段PQ和P′Q′互相平分.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:
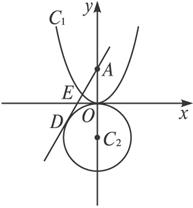
(1)证明(a+1)(y0+1)=1;
(2)若切线AD交抛物线C1于点E,且E为AD的中点,求点A纵坐标a.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com