
����Ŀ��2019��4�£�������У��ѧ���μ���ij���Ի������еĴ��������ִ�����У�μӿ��Ե�ѧ����ѧ�ɼ���100�ּ����ϵ��Ծ�����ϵͳ�����ķ�������ȡ��20���Ծ���������40���Ծ��ĵ÷����������µľ�Ҷͼ��
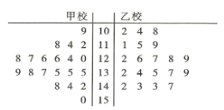
��1����ͨ����Ҷͼ�Ƚ���40���Ծ�����Уѧ����ѧ�ɼ�����λ����
��2��������ѧ�ɼ�������135�ֵļ�����ѧ�ɼ����㣬���ݾ�Ҷͼ�е����ݣ��ж��Ƿ���90![]() �İ�����Ϊ��ѧ�ɼ���100�ּ����ϵ�ѧ������ѧ�ɼ��Ƿ�����������ѧУ�йأ�
�İ�����Ϊ��ѧ�ɼ���100�ּ����ϵ�ѧ������ѧ�ɼ��Ƿ�����������ѧУ�йأ�
��3��������40��ѧ����ѡȡ��ѧ�ɼ���![]() ��ѧ�����÷ֲ�����ķ�ʽ�Ӽ�����У�г�ȡ5�ˣ��ٴ���5���������ȡ3�˷�����ʧ��ԭ������3����ǡ��2������Уѧ���ĸ��ʣ�
��ѧ�����÷ֲ�����ķ�ʽ�Ӽ�����У�г�ȡ5�ˣ��ٴ���5���������ȡ3�˷�����ʧ��ԭ������3����ǡ��2������Уѧ���ĸ��ʣ�
�ο���ʽ���ٽ�ֵ����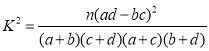 ������
������![]() ��
��
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
���𰸡�(1)��������(2)��������(3) ![]()
��������
��1�����ݾ�Ҷͼ�ֱ����������У��ѧ�ɼ�����λ������бȽϼ��ɵõ����ۣ���2�������������ݿɵ����������ɱ������ݵõ�![]() ���ɴ˿ɵý��ۣ���3�����ݷֲ�����ķ����ɵôӼ�У��ȡ2�ˡ���У��3�ˣ�Ȼ����ݹŵ��������⼴�ɣ�
���ɴ˿ɵý��ۣ���3�����ݷֲ�����ķ����ɵôӼ�У��ȡ2�ˡ���У��3�ˣ�Ȼ����ݹŵ��������⼴�ɣ�
��1���ɾ�Ҷͼ��֪����Уѧ����ѧ�ɼ�����λ��Ϊ![]() ����Уѧ����ѧ�ɼ�����λ��Ϊ
����Уѧ����ѧ�ɼ�����λ��Ϊ![]() ��
��
������40���Ծ��ijɼ�����Уѧ����ѧ�ɼ�����λ������Уѧ����ѧ�ɼ�����λ���ߣ�
��2�������⣬�õ�![]() ���������£�
���������£�
��У | ��У | �ϼ� | |
��ѧ�ɼ����� | 10 | 7 | 17 |
��ѧ�ɼ������� | 10 | 13 | 23 |
�ϼ� | 20 | 20 | 40 |
�ɱ������ݿɵã�![]() ��
��
����û��90![]() �İ�����Ϊ��ѧ�ɼ���100�ּ����ϵ�ѧ������ѧ�ɼ��Ƿ�����������ѧУ�йأ�
�İ�����Ϊ��ѧ�ɼ���100�ּ����ϵ�ѧ������ѧ�ɼ��Ƿ�����������ѧУ�йأ�
��3����40��ѧ������ѧ�ɼ���![]() �ļ�У��4�ˣ���У��6�ˣ��÷ֲ�����ķ�ʽ��ȡ5�ˣ����У��ȡ2�ˣ��ֱ����
�ļ�У��4�ˣ���У��6�ˣ��÷ֲ�����ķ�ʽ��ȡ5�ˣ����У��ȡ2�ˣ��ֱ����![]() ����У��3�ˣ��ֱ����
����У��3�ˣ��ֱ����![]() ��
��
����5���������ȡ3�ˣ����п��ܵĽ���У�![]()
![]() ����10�֣�
����10�֣�
������Уѧ��ǡ��2�˵Ľ���У�![]() ����6�֣�
����6�֣�
�����������![]() ��
��


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �У�����
�У�����![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�![]() ������
������![]() ����
����![]() ��
��![]() ,
,![]() ,
, ![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ���е㣬��
���е㣬��![]() ���߶�
���߶�![]() ��.
��.
������֤��ֱ��![]() ƽ��
ƽ��![]() ��
��
������![]() Ϊ
Ϊ![]() ���е㣬��ƽ��
���е㣬��ƽ��![]() ��ƽ��
��ƽ��![]() ���������ǵ�����ֵ��
���������ǵ�����ֵ��
������![]() ����
����![]() Ϊ��ֵʱ��ֱ��
Ϊ��ֵʱ��ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵΪ
���ɽǵ�����ֵΪ![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ⳤΪa��������ABCD��A1B1C1D1�У�PΪA1D1���е㣬QΪA1B1������һ�㣬E��FΪCD���������㣬��EF�ij�Ϊ��ֵ����������ĸ�ֵ�в�Ϊ��ֵ���ǣ� ��
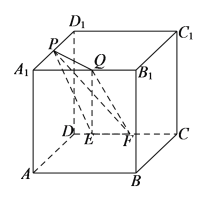
A.��P��ƽ��QEF�ľ���
B.ֱ��PQ��ƽ��PEF���ɵĽ�
C.����P��QEF�����
D.�����P��EF��Q�Ĵ�С
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣���![]() �У�
��![]() ��
��![]() ���е�Ϊ
���е�Ϊ![]() ����
����![]() ��
��![]() ���ӳ����ϣ���
���ӳ����ϣ���![]() .�̶���
.�̶���![]() ����ƽ�����ƶ�����
����ƽ�����ƶ�����![]() ��ʹ��Բ
��ʹ��Բ![]() �ֱ����
�ֱ����![]() ��
��![]() ���ӳ������У���ʼ����
���ӳ������У���ʼ����![]() ���ӳ��������ڵ�
���ӳ��������ڵ�![]() ���Ƕ���
���Ƕ���![]() �Ĺ켣Ϊ����
�Ĺ켣Ϊ����![]() .��
.��![]() ����ֱ��Ϊ
����ֱ��Ϊ![]() �ᣬ
�ᣬ![]() Ϊ����ԭ�㽨��ƽ��ֱ������ϵ����ͼ����ʾ.
Ϊ����ԭ�㽨��ƽ��ֱ������ϵ����ͼ����ʾ.
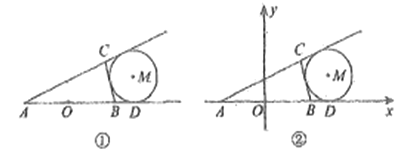
��1��������![]() �ķ��̣�
�ķ��̣�
��2������![]() ��ֱ��
��ֱ��![]() ������
������![]() ���ڲ�ͬ������
���ڲ�ͬ������![]() ��
��![]() ��ֱ��
��ֱ��![]() ��
��![]() �ֱ�����
�ֱ�����![]() �ڵ�
�ڵ�![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�����
�У�����![]() �IJ�������Ϊ
�IJ�������Ϊ![]()
![]() Ϊ����������ԭ��
Ϊ����������ԭ��![]() Ϊ���㣬��
Ϊ���㣬��![]() ��������Ϊ���Ὠ��������ϵ������
��������Ϊ���Ὠ��������ϵ������![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ������
������![]() ��
��![]() �Ĺ�����Ϊ
�Ĺ�����Ϊ![]() .
.
��������ֱ��![]() ��б�ʣ�
��б�ʣ�
��������![]() �ֱ�Ϊ����
�ֱ�Ϊ����![]() ��
��![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() ȡ���ֵʱ�����ı���
ȡ���ֵʱ�����ı���![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������������Σ��һֱ������19���ͣ�ֱ��1872�꣬�¹���ѧ�Ҵ��½�������Ե�Ҫ����������������ġ��ָ��������������ʷ�ƴ��½�ָ������ʵ�����۽������ϸ�Ŀ�ѧ�����ϣ��Ž���������������Ϊ����������ʱ����Ҳ�����˳���2000�������ѧʷ�ϵĵ�һ�δ�Σ������ν���½�ָ��ָ����������![]() ����Ϊ�����ǿյ��Ӽ�
����Ϊ�����ǿյ��Ӽ�![]() ��
��![]() ��������
��������![]() ��
��![]() ��
��![]() �е�ÿһ��Ԫ�ض�С��
�е�ÿһ��Ԫ�ض�С��![]() �е�ÿһ��Ԫ�أ����
�е�ÿһ��Ԫ�أ����![]() Ϊ���½�ָ�.���жϣ�������һ���½�ָ�
Ϊ���½�ָ�.���жϣ�������һ���½�ָ�![]() ������ѡ���У����ܳ�������____��
������ѡ���У����ܳ�������____��
��![]() û�����Ԫ�أ�
û�����Ԫ�أ�![]() ��һ����СԪ�أ���
��һ����СԪ�أ���![]() û�����Ԫ�أ�
û�����Ԫ�أ�![]() Ҳû����СԪ�أ�
Ҳû����СԪ�أ�
��![]() ��һ�����Ԫ�أ�
��һ�����Ԫ�أ�![]() ��һ����СԪ�أ���
��һ����СԪ�أ���![]() ��һ�����Ԫ�أ�
��һ�����Ԫ�أ�![]() û����СԪ��.
û����СԪ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l��![]() ��������C��
��������C��![]() �Ľ���F������������C���ڵ�A��B���㣬��A��B����ֱ����������ߵĴ��ߣ�����ֱ�ΪM��N��������˵���������
�Ľ���F������������C���ڵ�A��B���㣬��A��B����ֱ����������ߵĴ��ߣ�����ֱ�ΪM��N��������˵���������![]() ����
����![]()
A. �����ߵķ���Ϊ![]() B. �߶�AB�ij���Ϊ
B. �߶�AB�ij���Ϊ![]()
C. ![]() D. �߶�AB���е㵽y��ľ���Ϊ
D. �߶�AB���е㵽y��ľ���Ϊ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�����ABCD�������Σ�����
�У�����ABCD�������Σ�����![]() ����ABCD����
����ABCD����![]() ����E��F�ֱ�ΪPC��BD���е㣮
����E��F�ֱ�ΪPC��BD���е㣮
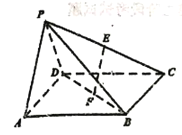
��1����֤��![]() ƽ��PAD��
ƽ��PAD��
��2����ֱ��EF��ƽ��PBD���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com