
����Ŀ��ij��ʳƷҩƷ�ල�����ֿ�չ2019�괺��У������ȫ��飬�Ա��е�8����ѧʳ�ý�����ԭ�ϲɹ��ӹ������������ļ������֣�������������±���ʾ��
��ѧ��� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
ԭ�ϲɹ��ӹ�������x | 100 | 95 | 93 | 83 | 82 | 75 | 70 | 66 |
����������y | 87 | 84 | 83 | 82 | 81 | 79 | 77 | 75 |
��1����֪x��y֮�����������ع�ϵ����y����x�����Իع鷽�̣�����ȷ��0.1��
��2���ִ�8����������ѧʳ���������ȡ�������һ�飬��������ѧʳ�õ�ԭ�ϲɹ��ӹ����������������־�����80�֣�����ɡ��Աȱ��ʳ�á�������鱻��Ϊ���Աȱ��ʳ�á��ĸ���.
�ο���ʽ��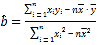 ��
��![]() ��
��
�ο����ݣ�![]() ��
��![]() .
.
���𰸡���1��![]() ����2��
����2��![]()
��������
��1�����������![]() ��
��![]() ������ع�ϵ����д�����Իع鷽�̣�
������ع�ϵ����д�����Իع鷽�̣�
��2�����оٷ�д�������¼�������������ĸ���ֵ��
��1��������ã�![]() ��
��![]() ��
��
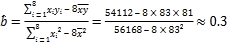 ��
��
![]() .
.
����������Իع鷽��Ϊ��![]() .
.
��2����8����ѧʳ������ѡ���������й�28�ֽ����
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
����ԭ�ϲɹ��ӹ��������ֺ������������־�����80�ֵ���10�ֽ����
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
���Ը��鱻��Ϊ���Աȱ��ʳ�á��ĸ���Ϊ![]() .
.


 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڲ�ͬ��ֱ��![]() �벻ͬ��ƽ��
�벻ͬ��ƽ��![]() ���������������⣺
���������������⣺
����![]() ��
��![]() ��
��
����![]() ��
��![]() ��
��
����![]() ��
��![]() ��
��![]() ��
��
����![]() ��
��![]() ��
��![]() ��
��
����![]() ��
��![]() ��
��![]() ��
��
����![]() ��
��![]() ��
��![]() ��
��
������ȷ����������__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У�
��![]() ��
��![]() ��
��![]() ���ضԽ���
���ضԽ���![]() ��
��![]() ����ʹ��
����ʹ��![]() ��ƽ��
��ƽ��![]() �ڵ���Ӱ
�ڵ���Ӱ![]() ǡ��
ǡ��![]() ��.
��.


������֤��![]() ��
��![]() ��
��
����������ֱ��![]() ��
��![]() ���ɵĽǣ�
���ɵĽǣ�
����������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����˫����![]() �ķ���Ϊ
�ķ���Ϊ![]() .
.
��1����![]() �Ǿ�����
�Ǿ�����![]() ��ֱ�ߣ��Һ�
��ֱ�ߣ��Һ�![]() ���ҽ���һ�������㣬��
���ҽ���һ�������㣬��![]() �ķ��̣�
�ķ��̣�
��2����![]() ��
��![]() ��һ�������ߣ�
��һ�������ߣ�![]() ��
��![]() ��
��![]() �����������.����
�����������.����![]() ��
��![]() �ϵ�һ�㣬
�ϵ�һ�㣬![]() ���ڵ�
���ڵ�![]() �ĶԳƵ��Ϊ
�ĶԳƵ��Ϊ![]() ��
��![]() ���ڵ�
���ڵ�![]() �ĶԳƵ��Ϊ
�ĶԳƵ��Ϊ![]() .���жϵ�
.���жϵ�![]() �Ƿ������
�Ƿ������![]() �ϣ���˵������.
�ϣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����֪![]() ,
,![]() ,
,![]() ,�÷�֤��֤����
,�÷�֤��֤����![]() ��������һ����С��
��������һ����С��![]() ;
;
��2������ѧ���ɷ�֤����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���A��B��C��Ӧ�ı߷ֱ���a��b��c����2acosBcosC+2ccosAcosB��b=0.
��1�����B�Ĵ�С��
��2������ABC�����S=3![]() ��a=3����sinAsinC��ֵ.
��a=3����sinAsinC��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �Ķ���Ϊ
�Ķ���Ϊ![]() ������
������![]() Ϊ
Ϊ![]() .
.
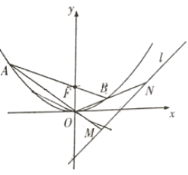
��1����������![]() �ķ��̣�
�ķ��̣�
��2������![]() ��ֱ�߽�������
��ֱ�߽�������![]() ��
��![]() ��
��![]() ���㣬��ֱ��
���㣬��ֱ��![]() ��
��![]() �ֱ�ֱ��
�ֱ�ֱ��![]() ��
��![]() ��
��![]() ���㣬��
���㣬��![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����Ȳ�����![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ����
����![]() ����
����![]() �ɵȱ�����.
�ɵȱ�����.
��1����![]() ��ͨ�ʽ��
��ͨ�ʽ��
��2����![]() ��������
��������![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ����
����![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com