
���� ��1���Ѽ����귽�̻�Ϊֱ�����귽�̣��������ɵó���
��2����t1��t2Ϊ��Ӧ����ֵt2+6tcos��+7=0������0��cos2����$\frac{7}{9}$�����ø���ϵ���Ĺ�ϵ�ɵ�|PA|2+|PB|2=��-6cos����2-14���ɵó���
��� �⣺��1������C�ķ�����$��=2\sqrt{2}sin����-\frac{��}{4}��$����Ϊ��2=2��sin��-2��cos�ȣ�
��x2+y2=2y-2x��
����C�ķ���Ϊ��x+1��2+��y-1��2=2��
����=0ʱ��ֱ��l��y=1��
��������C�ɵ�x+1=��2�����x=1��-3��
��|AB|=4��
��2����t1��t2Ϊ��Ӧ����ֵt2+6tcos��+7=0������0����cos2����$\frac{7}{9}$
��t1+t2=-6cos����t1t2=7��
��|PA|2+|PB|2=��-6cos����2-14��
��|PA|2+|PB|2�ʣ�14��22]��
���� ���⿼���˰Ѽ����귽�̻�Ϊֱ�����귽�̡�һԪ���η��̵ĸ���ϵ���Ĺ�ϵ�������ļ������壬������������������������������е��⣮


 ��У���һ��ͨϵ�д�
��У���һ��ͨϵ�д� �γ̴����Ծ�����100��ϵ�д�
�γ̴����Ծ�����100��ϵ�д� �¾�����ĩ���100��ϵ�д�
�¾�����ĩ���100��ϵ�д� ȫ�ܴ���100��ϵ�д�
ȫ�ܴ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
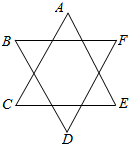 ��4�ֲ�ͬ����ɫ��ͼ��A��B��C��D��E��F���������Ⱦɫ��Ҫ��ͬһ�߶ε����㣨�磺AC��BD��������ɫ����ͬ���������ڵ����㣨�磺AB��BC��������ɫҲ����ͬ����ͬ��Ⱦɫ��������Ϊ96 ������ѧ���𣩣�
��4�ֲ�ͬ����ɫ��ͼ��A��B��C��D��E��F���������Ⱦɫ��Ҫ��ͬһ�߶ε����㣨�磺AC��BD��������ɫ����ͬ���������ڵ����㣨�磺AB��BC��������ɫҲ����ͬ����ͬ��Ⱦɫ��������Ϊ96 ������ѧ���𣩣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{7}{24}$ | B�� | $\frac{{3\sqrt{7}}}{8}$ | C�� | $\frac{{\sqrt{2}}}{4}$ | D�� | $\frac{{\sqrt{14}}}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
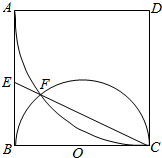 ��ͼ���ı���Ϊ�߳�Ϊa�������Σ���DΪԲ�ģ�DAΪ�뾶��Բ������BCΪֱ����ԲO����C��F������CF���ӳ���AB�ڵ�E��
��ͼ���ı���Ϊ�߳�Ϊa�������Σ���DΪԲ�ģ�DAΪ�뾶��Բ������BCΪֱ����ԲO����C��F������CF���ӳ���AB�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | M��-1��1����r=2 | B�� | M��-1��1����r=4 | C�� | M��1��-1����r=2 | D�� | M��1��-1����r=4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�6] | B�� | ��-�ޣ�6�� | C�� | ��0��6] | D�� | [6��+�ޣ� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com