
【题目】从甲、乙两名学生中选拔一人参加射击比赛,对他们的射击水平进行了测试,两人在相同条件下各射击10次,命中的环数如下:
甲:7,8,6,9,6,5,9,9,7,4.
乙:9,5,7,8,7,6,8,6,7,7.
(1)分别计算甲、乙两人射击命中环数的极差、众数和中位数;
(2)分别计算甲、乙两人射击命中环数的平均数、方差、标准差;
(3)比较两人的成绩,然后决定选择哪一个人参赛.
科目:高中数学 来源: 题型:
【题目】高一某班级在学校数学嘉年华活动中推出了一款数学游戏,受到大家的一致追捧.游戏规则如下:游戏参与者连续抛掷一颗质地均匀的骰子,记第i次得到的点数为![]() ,若存在正整数n,使得
,若存在正整数n,使得![]() ,则称为游戏参与者的幸运数字。
,则称为游戏参与者的幸运数字。
(I)求游戏参与者的幸运数字为1的概率;
(Ⅱ)求游戏参与者的幸运数字为2的概率,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面ABCD为平行四边形,PA⊥底面ABCD,
中,底面ABCD为平行四边形,PA⊥底面ABCD,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求证:平面PCA⊥平面PCD;
(2)设E为侧棱PC上的一点,若直线BE与底面ABCD所成的角为45°,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人独立的对某一技术难题进行攻关。甲能攻克的概率为![]() ,乙能攻克的概率为
,乙能攻克的概率为![]() ,丙能攻克的概率为
,丙能攻克的概率为![]() ;
;
(1)求这一技术难题被攻克的概率;
(2)若该技术难题未被攻克,上级不做任何奖励;若该技术难题被攻克,上级会奖励6万元。奖励规则如下:若只有一人攻克,则此人获得全部奖金6万元;若只有2人攻克,则此二人均分奖金,每人3万元;若三人均攻克,则每人2万元。在这一技术难题被攻克的前提下,设甲拿到的奖金数为![]() ,求
,求![]() 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“每天锻炼一小时,健康工作五十年,幸福生活一辈子.”一科研单位为了解员工爱好运动是否与性别有关,从单位随机抽取30名员工进行了问卷调查,得到了如下列联表:
男性 | 女性 | 合计 | |
爱好 | 10 | ||
不爱好 | 8 | ||
合计 | 30 |
已知在这30人中随机抽取1人抽到爱好运动的员工的概率是![]() .
.
(1)请将上面的列联表补充完整(在答题卷上直接填写结果,不需要写求解过程),并据此资料分析能否有把握认为爱好运动与性别有关?
(2)若从这30人中的女性员工中随机抽取2人参加一活动,记爱好运动的人数为![]() ,求
,求![]() 的分布列、数学期望.参考数据:
的分布列、数学期望.参考数据:
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为椭圆E:
为椭圆E: ![]() 的左、右顶点,
的左、右顶点, ![]() ,E的两个焦点与E的短轴两个端点所构成的四边形是正方形.
,E的两个焦点与E的短轴两个端点所构成的四边形是正方形.
(1)求椭圆E的方程;
(2)设动点![]() (
(![]() ),记直线
),记直线![]() 与E的交点(不同于
与E的交点(不同于![]() )到x轴的距离分别为
)到x轴的距离分别为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线![]() ,直线
,直线![]() 关于直线
关于直线![]() 对称的直线为
对称的直线为![]() ,直线
,直线![]() ,
,![]() 与曲线
与曲线![]() 分别交于点
分别交于点![]() 、
、![]() 和
和![]() 、
、![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)当![]() 变化时,试问直线
变化时,试问直线![]() 是否恒过定点?若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.
是否恒过定点?若恒过定点,求出该定点坐标;若不恒过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为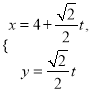 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, ![]() 轴的非负半轴为极轴建立极坐标系,圆
轴的非负半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(1)求圆![]() 的直角坐标方程及弦
的直角坐标方程及弦![]() 的长;
的长;
(2)动点![]() 在圆
在圆![]() 上(不与
上(不与![]() ,
, ![]() 重合),试求
重合),试求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,第1个图形由正三角形扩展而成,共12个顶点.第n个图形是由正n+2边形扩展而来 ![]() ,则第n+1个图形的顶点个数是 ( )
,则第n+1个图形的顶点个数是 ( )
 (1)
(1)  (2)
(2) (3)
(3) 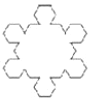 (4)
(4)
A. (2n+1)(2n+2)B. 3(2n+2)C. (n+2)(n+3)D. (n+3)(n+4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com