
【题目】某旅游景区的景点![]() 处和
处和![]() 处之间有两种到达方式,一种是沿直线步行,另一种是沿索道乘坐缆车,现有一名游客从
处之间有两种到达方式,一种是沿直线步行,另一种是沿索道乘坐缆车,现有一名游客从![]() 处出发,以
处出发,以![]() 的速度匀速步行,
的速度匀速步行,![]() 后到达
后到达![]() 处,在
处,在![]() 处停留
处停留![]() 后,再乘坐缆车回到
后,再乘坐缆车回到![]() 处.假设缆车匀速直线运动的速度为
处.假设缆车匀速直线运动的速度为![]() .
.
(1)求该游客离景点![]() 的距离
的距离![]() 关于出发后的时间
关于出发后的时间![]() 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)做出(1)中函数的图象,并求该游客离景点![]() 的距离不小于
的距离不小于![]() 的总时长.
的总时长.
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】1998年,某地在抗洪抢险中接到预报,24小时后有一个超历史最高水位的洪峰到达,为保万无一失,指挥部决定在24小时内筑起一道堤坝作为第二防线.经计算,其工程量除动用现有军民连续奋战外,还需要20台大型翻斗车同时作业24小时.但是,除了第一辆车可以立即调入工作外,其余车辆需从各单位紧急抽调,每隔20分钟有一辆车到达投入作业,已知指挥部最多能组织到25辆车.问24小时内能否完成第二防线工程?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着“一带一路”倡议的推进,中国与沿线国家旅游合作越来越密切,中国到“一带一路”沿线国家的游客人也越来越多,如图是2013-2018年中国到“一带一路”沿线国家的游客人次情况,则下列说法正确的是( )
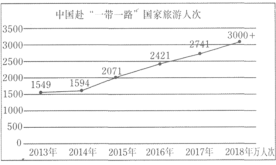
①2013-2018年中国到“一带一路”沿线国家的游客人次逐年增加
②2013-2018年这6年中,2016年中国到“一带一路”沿线国家的游客人次增幅最小
③2016-2018年这3年中,中国到“一带一路”沿线国家的游客人次每年的增幅基本持平
A.①③B.②③C.①②D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为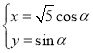 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,求
上,求![]() 的最小值及此时
的最小值及此时![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,写出函数
时,写出函数![]() 的单调区间;(直接写出答案,不必写出证明过程)
的单调区间;(直接写出答案,不必写出证明过程)
(2)当![]() 时,求函数
时,求函数![]() 的零点;
的零点;
(3)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最小值.
上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周上有![]() 个点
个点![]() ,用弦两两连结起来,其中任何3条弦都不在圆内共点.现将由此形成的互补重叠的圆内区域的个数记为
,用弦两两连结起来,其中任何3条弦都不在圆内共点.现将由此形成的互补重叠的圆内区域的个数记为![]() .
.
(1).直接画图求出![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(2).确定![]() 的表达式.
的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com