
【题目】如图,四棱锥P﹣ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
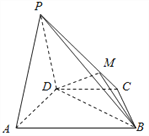
(1)求证:AP∥平面MBD;
(2)若AD⊥PB,求证:BD⊥平面PAD.
 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】某研究小组在电脑上进行人工降雨模拟实验,准备用![]() 、
、![]() 、
、![]() 三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其试验数据统计如表:
三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其试验数据统计如表:
方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验总次数 |
| 甲 | 4次 | 6次 | 2次 | 12次 |
| 乙 | 3次 | 6次 | 3次 | 12次 |
| 丙 | 2次 | 2次 | 8次 | 12次 |
假定对甲、乙、丙三地实施的人工降雨彼此互不影响,请你根据人工降雨模拟实验的统计数据:
(Ⅰ)求甲、乙、丙三地都恰为中雨的概率;
(Ⅱ)考虑到旱情和水土流失,如果甲地恰需中雨即达到理想状态,乙地必须是大雨才达到理想状态,丙地只能是小雨或中雨即达到理想状态,记“甲、乙、丙三地中达到理想状态的个数”为随机变量![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD 中,AB∥CD ,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别为CD和PC的中点.求证:
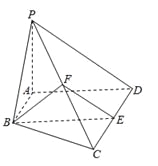
(1)BE∥平面PAD;
(2)平面BEF⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市组织500名志愿者参加敬老活动,为方便安排任务将所有志愿者按年龄(单位:岁)分组,得到的频率分布表如下.现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人担任联系人.
年龄(岁) | 频率 | |
第1组 | [25,30) | 0.1 |
第2组 | [30,35) | 0.1 |
第3组 | [35,40) | 0.4 |
第4组 | [40,45) | 0.3 |
第5组 | [45,50) | 0.1 |
(I)应分别在第1,2,3组中抽取志愿者多少人?
(II)从这6人中随机抽取2人担任本次活动的宣传员,求至少有1人年龄在第3组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校收集该校学生从家到学校的时间后,制作成如下的频率分布直方图:
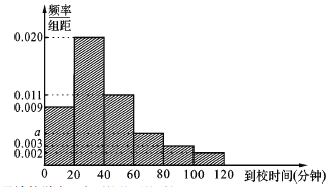
(1)求![]() 的值及该校学生从家到校的平均时间;
的值及该校学生从家到校的平均时间;
(2)若该校因学生寝室不足,只能容纳全校![]() 的学生住校,出于安全角度考虑,从家到校时间较长的学生才住校,请问从家到校时间多少分钟以上开始住校.
的学生住校,出于安全角度考虑,从家到校时间较长的学生才住校,请问从家到校时间多少分钟以上开始住校.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在以![]() 为顶点的五面体中,O为AB的中点,
为顶点的五面体中,O为AB的中点,
![]() 平面
平面![]() ,
, ![]() ∥
∥![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(1)在图中过点O作平面![]() ,使得
,使得![]() ∥平面
∥平面![]() ,并说明理由;
,并说明理由;
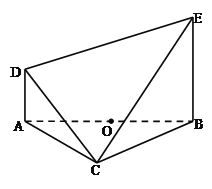
(2)求直线DE与平面CBE所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
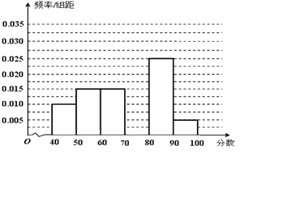
【题目】某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,60), ...,[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ) 从成绩在[40,50)和[90,100]的学生中任选两人,求他们在同一分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是偶函数,对于x∈R都有f(x+6)=f(x)+f(3)成立.当x1,x2∈[0,3],且x1≠x2时,都有![]() >0,给出下列命题:
>0,给出下列命题:
① f(3)=0;
② 直线x=-6是函数y=f(x)的图象的一条对称轴;
③ 函数y=f(x)在[-9,-6]上为单调递减函数;
④ 函数y=f(x)在[-9,9]上有4个零点.
其中正确的命题是____________.(填序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() .
.
(1)求函数![]() 的单调增区间;
的单调增区间;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数![]() 的图象,若
的图象,若![]() 在
在![]() 上至少含有10个零点,求
上至少含有10个零点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com