
【题目】已知函数f(x)=ax2+(x﹣1)ex .
(1)当a=﹣ ![]() 时,求f(x)在点P(1,f(1))处的切线方程;
时,求f(x)在点P(1,f(1))处的切线方程;
(2)讨论f(x)的单调性;
(3)当﹣ ![]() <a<﹣
<a<﹣ ![]() 时,f(x)是否存在极值?若存在,求所有极值的和的取值范围.
时,f(x)是否存在极值?若存在,求所有极值的和的取值范围.
【答案】
(1)解:当a= ![]() 时,f(x)=
时,f(x)= ![]() x2+(x﹣1)ex,
x2+(x﹣1)ex,
∴f(1)= ![]() ,
,
f′(x)=﹣(e+1)x+xex,∴f′(1)=﹣1
切线方程为:y+ ![]() =﹣(x﹣1),
=﹣(x﹣1),
即:2x+2y+e﹣1=0
(2)解:f′(x)=2ax+xex=x(ex+2a)
①当2a≥0即a≥0时,f(x)在(﹣∞,0)上单调递减,在(0,+∞)上单调递增;
②当﹣ ![]() <a<0时,f(x)在(﹣∞,ln(﹣2a))上单调递增,
<a<0时,f(x)在(﹣∞,ln(﹣2a))上单调递增,
在(ln(﹣2a),0)上单调递减,在(0,+∞)上单调递增;
③当a=﹣ ![]() 时,f(x)在(﹣∞,+∞)上单调递增;
时,f(x)在(﹣∞,+∞)上单调递增;
④当a<﹣ ![]() 时,f(x)在(﹣∞,0))上单调递增,
时,f(x)在(﹣∞,0))上单调递增,
在(0,ln(﹣2a))上单调递减,在(ln(﹣2a),+∞)上单调递增
(3)解:由(2)知,当﹣ ![]() <a<﹣
<a<﹣ ![]() <0时,
<0时,
f(x)在(﹣∞,ln(﹣2a))上单调递增,在(ln(﹣2a),0)上单调递减,在(0,+∞)上单调递增,
∴x1=ln(﹣2a)为极大值点,x2=0为极小值点,所有极值的和即为f(x1)+f(x2),
f(x1)+f(x2)=ax12+(x1﹣1) ![]() ﹣1
﹣1
∵x1=ln(﹣2a),∴a=﹣ ![]()
![]() ,
,
∴f(x1)+f(x2)=﹣ ![]()
![]() x12+(x1﹣1)
x12+(x1﹣1) ![]() ﹣1=
﹣1= ![]() (﹣
(﹣ ![]() x12+x1﹣1)﹣1
x12+x1﹣1)﹣1
∵﹣ ![]() <a<﹣
<a<﹣ ![]() ,∴
,∴ ![]() <﹣2a<1,∴﹣1<x1=ln(﹣2a)<0,
<﹣2a<1,∴﹣1<x1=ln(﹣2a)<0,
令(x)=ex (﹣ ![]() x2+x﹣1)﹣1(﹣1<x<0)
x2+x﹣1)﹣1(﹣1<x<0)
∴′(x)=ex (﹣ ![]() x2)<0∴(x)在(﹣1,0)单调递减
x2)<0∴(x)在(﹣1,0)单调递减
∴(0)<(x)<(﹣1)
即﹣2<(x)<﹣ ![]() ﹣1
﹣1
∴所有极值的和的取值范围为(﹣2,﹣ ![]() )
)
【解析】(1)当a= ![]() 时,求出f′(x)=﹣(e+1)x+xex , 利用导数的几何意义能出f(x)在点P(1,f(1))处的切线方程.(2)f′(x)=2ax+xex=x(ex+2a),由此根据a≥0,﹣
时,求出f′(x)=﹣(e+1)x+xex , 利用导数的几何意义能出f(x)在点P(1,f(1))处的切线方程.(2)f′(x)=2ax+xex=x(ex+2a),由此根据a≥0,﹣ ![]() <a<0,a=﹣
<a<0,a=﹣ ![]() ,a<﹣
,a<﹣ ![]() ,利用导数性质能讨论f(x)的单调性.(3)推导出x1=ln(﹣2a)为极大值点,x2=0为极小值点,所有极值的和即为f(x1)+f(x2),f(x1)+f(x2)=ax12+(x1﹣1)
,利用导数性质能讨论f(x)的单调性.(3)推导出x1=ln(﹣2a)为极大值点,x2=0为极小值点,所有极值的和即为f(x1)+f(x2),f(x1)+f(x2)=ax12+(x1﹣1) ![]() ﹣1,由此利用导性质能求出所有极值的和的取值范围.
﹣1,由此利用导性质能求出所有极值的和的取值范围.
【考点精析】利用函数的极值与导数对题目进行判断即可得到答案,需要熟知求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且对任意正整数n,都有3an=2Sn+3成立.
(1)求数列{an}的通项公式;
(2)设bn=log3an , 求数列{ ![]() }的前n项和Tn .
}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC﹣A1B1C1中,∠ABC=90°,E、F分别为A1C1、B1C1的中点,D为棱CC1上任一点.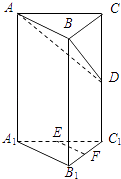
(Ⅰ)求证:直线EF∥平面ABD;
(Ⅱ)求证:平面ABD⊥平面BCC1B1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=6cos2![]() +
+![]() sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.
sinωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B、C为图象与x轴的交点,且△ABC为正三角形.

(1)求ω的值及函数f(x)的值域;
(2)若f(x0)=![]() ,且x0∈(-
,且x0∈(-![]() ,
,![]() ),求f(x0+1)的值.
),求f(x0+1)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+(x﹣1)ex .
(1)当a=﹣ ![]() 时,求f(x)在点P(1,f(1))处的切线方程;
时,求f(x)在点P(1,f(1))处的切线方程;
(2)讨论f(x)的单调性;
(3)当﹣ ![]() <a<﹣
<a<﹣ ![]() 时,f(x)是否存在极值?若存在,求所有极值的和的取值范围.
时,f(x)是否存在极值?若存在,求所有极值的和的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com