
(2004
全国,20)如下图,已知四棱锥P-ABCD,PB⊥AD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,侧面PAD与底面ABCD所成的二面角为120°.(1)
求点P到平面ABCD的距离;(2)
求面APB与面CPB所成二面角的大小.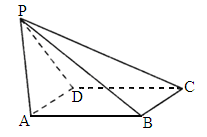
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:全优设计必修五数学苏教版 苏教版 题型:022
2004年的震惊全国的阜阳奶粉事件中,劣质奶粉的蛋白质含量远远低于国家质量标准(蛋白质含量应为10%-20%),若劣质奶粉的蛋白质的含量为p,则p________10%;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com