
【题目】某中学的甲、乙、丙三名同学参加高校自主招生考试,每位同学彼此独立的从![]() 五所高校中任选2所.
五所高校中任选2所.
(1)求甲、乙、丙三名同学都选![]() 高校的概率;
高校的概率;
(2)若已知甲同学特别喜欢![]() 高校,他必选
高校,他必选![]() 校,另在
校,另在![]() 四校中再随机选1所;而同学乙和丙对五所高校没有偏爱,因此他们每人在五所高校中随机选2所.
四校中再随机选1所;而同学乙和丙对五所高校没有偏爱,因此他们每人在五所高校中随机选2所.
(i)求甲同学选![]() 高校且乙、丙都未选
高校且乙、丙都未选![]() 高校的概率;
高校的概率;
(ii)记![]() 为甲、乙、丙三名同学中选
为甲、乙、丙三名同学中选![]() 高校的人数,求随机变量
高校的人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
【答案】(1)![]() (2)(i)
(2)(i)![]() (ii)分布列见解析,
(ii)分布列见解析,![]()
【解析】
(1)先计算甲、乙、丙同学分别选择D高校的概率,利用事件的独立性即得解;
(2)(i)分别计算每个事件的概率,再利用事件的独立性即得解;
(ii)![]() ,利用事件的独立性,分别计算对应的概率,列出分布列,计算数学期望即得解.
,利用事件的独立性,分别计算对应的概率,列出分布列,计算数学期望即得解.
(1)甲从![]() 五所高校中任选2所,共有
五所高校中任选2所,共有![]()
![]() 共10种情况,
共10种情况,
甲、乙、丙同学都选![]() 高校,共有
高校,共有![]() 四种情况,
四种情况,
甲同学选![]() 高校的概率为
高校的概率为![]() ,
,
因此乙、丙两同学选![]() 高校的概率为
高校的概率为![]() ,
,
因为每位同学彼此独立,
所以甲、乙、丙三名同学都选![]() 高校的概率为
高校的概率为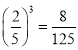 .
.
(2)(i)甲同学必选![]() 校且选
校且选![]() 高校的概率为
高校的概率为![]() ,乙未选
,乙未选![]() 高校的概率为
高校的概率为![]() ,
,
丙未选![]() 高校的概率为
高校的概率为![]() ,因为每位同学彼此独立,
,因为每位同学彼此独立,
所以甲同学选![]() 高校且乙、丙都未选
高校且乙、丙都未选![]() 高校的概率为
高校的概率为![]() .
.
(ii)![]() ,
,
因此![]()
![]()
![]() ,
,
![]() .
.
即![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
因此数学期望为
![]() .
.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() ,O为坐标原点,F为C的右焦点,过F的直线与C的两条渐近线的交点分别为M、N.若
,O为坐标原点,F为C的右焦点,过F的直线与C的两条渐近线的交点分别为M、N.若![]() OMN为直角三角形,则|MN|=
OMN为直角三角形,则|MN|=
A. ![]() B. 3 C.
B. 3 C. ![]() D. 4
D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:![]() 过点
过点![]() ,过抛物线E上一点
,过抛物线E上一点![]() 作两直线PM,PN与圆C:
作两直线PM,PN与圆C:![]() 相切,且分别交抛物线E于M、N两点.
相切,且分别交抛物线E于M、N两点.
(1)求抛物线E的方程,并求其焦点坐标和准线方程;
(2)若直线MN的斜率为![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
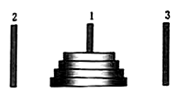
【题目】如图所示,有三根针和套在一根针上的![]() 个金属片,按下列规则,把金属片从一根针上全部移到另一根针上.
个金属片,按下列规则,把金属片从一根针上全部移到另一根针上.
(1)每次只能移动一个金属片;
(2)在每次移动过程中,每根针上较大的金属片不能放在较小的金属片上面.
将![]() 个金属片从1号针移到3号针最少需要移动的次数记为
个金属片从1号针移到3号针最少需要移动的次数记为![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点为极点,![]() 轴的非负半轴为极轴,建立极坐标系,并在两种坐标系中取相同的长度单位.已知曲线
轴的非负半轴为极轴,建立极坐标系,并在两种坐标系中取相同的长度单位.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),射线
),射线![]() ,
,![]() ,
,![]() 分别与曲线
分别与曲线![]() 交于极点
交于极点![]() 外的三点
外的三点![]() .
.
(1)求![]() 的值;
的值;
(2)当![]() 时,
时,![]() 两点在曲线
两点在曲线![]() 上,求
上,求![]() 与
与![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为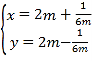 (m为参数),以坐标点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ+
(m为参数),以坐标点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ+![]() )=1.
)=1.
(1)求直线l的直角坐标方程和曲线C的普通方程;
(2)已知点M (2,0),若直线l与曲线C相交于P、Q两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列![]() 的前
的前![]() 项中的最大项为
项中的最大项为![]() ,最小项为
,最小项为![]() ,设
,设![]()
(1)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)若数列![]() 是等差数列,求证:数列
是等差数列,求证:数列![]() 是等差数列.
是等差数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com