
【题目】如图,四边形![]() 是边长为2的菱形,且
是边长为2的菱形,且![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上任意一点.
上任意一点.
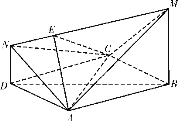
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 的最大值是
的最大值是![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)见证明;(2) ![]()
【解析】
(1)推导出AC⊥BM,AC⊥BD,得AC⊥平面BMND,从而可得到证明;(2)由AE=CE和余弦定理可知,当AE最短即AE⊥MN,CE⊥MN时∠AEC最大,取MN中点H,连接H与AC、BD的交点O,知OH⊥平面ABCD,分别以直线![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,设
轴建立空间直角坐标系,设![]() ,利用二面角
,利用二面角![]() 的平面角为
的平面角为![]() ,可求出a,然后利用VM﹣NAC=VM﹣EAC+VN﹣EAC可得结果.
,可求出a,然后利用VM﹣NAC=VM﹣EAC+VN﹣EAC可得结果.
(1)因为![]() 平面
平面![]() ,则
,则![]() .
.
又四边形![]() 是菱形,则
是菱形,则![]() ,又
,又![]() ,
,
所以![]() 平面
平面![]() ,因为AC在平面
,因为AC在平面![]() 内,
内,
所以平面![]() 平面
平面![]() .
.
(2)设![]() 与
与![]() 的交点为
的交点为![]() ,连结
,连结![]() . 因为
. 因为![]() 平面
平面![]() ,则
,则![]() ,又
,又![]() 为
为![]() 的中点,则
的中点,则![]() ,由余弦定理得
,由余弦定理得![]() ,
,![]() .当AE最短时∠AEC最大,此时
.当AE最短时∠AEC最大,此时![]() ,
,![]() ,
,![]() ,因为AC=2,
,因为AC=2,![]() ,OE=
,OE=![]() . 取MN的中点H,分别以直线
. 取MN的中点H,分别以直线![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
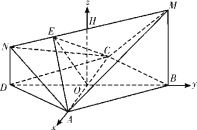
设![]() ,则点
,则点![]() ,
,![]()
![]() ,
,![]() ,
,![]() .设平面
.设平面![]() 的法向量
的法向量![]() ,
,
则 ,即
,即![]() ,取
,取![]() ,则
,则![]() ,
,
同理求得平面![]() 的法向量
的法向量![]() .
.
因为![]() 是二面角
是二面角 ![]() 的平面角,则
的平面角,则
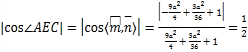 ,解得
,解得![]() 或
或![]() .
.
由图可知a<OE=![]() ,故
,故![]() (舍去),
(舍去),![]() ,
,
因为![]() ,
,![]() ,
,![]() ,
,
则![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)和y=g(x)在[-2,2]的图像如图所示,给出下列四个命题:

①方程f[g(x)]=0有且仅有6个根
②方程g[f(x)]=0有且仅有3个根
③方程f[f(x)]=0有且仅有5个根
④方程g[g(x)]=0有且仅有4个根
其中正确的命题是___
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,给定
,给定![]() 个整点
个整点![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,从上面的
时,从上面的![]() 个整点中任取两个不同的整点
个整点中任取两个不同的整点![]() ,求
,求![]() 的所有可能值;
的所有可能值;
(Ⅱ)从上面![]() 个整点中任取
个整点中任取![]() 个不同的整点,
个不同的整点,![]() .
.
(i)证明:存在互不相同的四个整点![]() ,满足
,满足![]() ,
,![]() ;
;
(ii)证明:存在互不相同的四个整点![]() ,满足
,满足![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种“笼具”由内,外两层组成,无下底面,内层和外层分别是一个圆锥和圆柱,其中圆柱与圆锥的底面周长相等,圆柱有上底面,制作时需要将圆锥的顶端剪去,剪去部分和接头忽略不计,已知圆柱的底面周长为![]() ,高为
,高为![]() ,圆锥的母线长为
,圆锥的母线长为![]() .
.
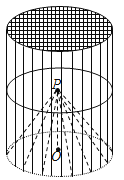
(1)求这种“笼具”的体积(结果精确到0.1![]() );
);
(2)现要使用一种纱网材料制作50个“笼具”,该材料的造价为每平方米8元,共需多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究国民收入在国民之间的分配,避免贫富过分悬殊,美国统计学家劳伦茨提出了著名的劳伦茨曲线,如图所示.劳伦茨曲线为直线![]() 时,表示收入完全平等,劳伦茨曲线为折线
时,表示收入完全平等,劳伦茨曲线为折线![]() 时,表示收入完全不平等.记区域
时,表示收入完全不平等.记区域![]() 为不平等区域,
为不平等区域,![]() 表示其面积,
表示其面积,![]() 为
为![]() 的面积.将
的面积.将![]() ,称为基尼系数.对于下列说法:
,称为基尼系数.对于下列说法:
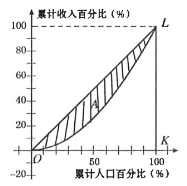
①![]() 越小,则国民分配越公平;
越小,则国民分配越公平;
②设劳伦茨曲线对应的函数为![]() ,则对
,则对![]() ,均有
,均有![]() ;
;
③若某国家某年的劳伦茨曲线近似为![]() ,则
,则![]() ;
;
其中正确的是:( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com