
【题目】已知函数f(x)=cos ![]() ,g(x)=exf(x),其中e为自然对数的底数.
,g(x)=exf(x),其中e为自然对数的底数.
(1)求曲线y=g(x)在点(0,g(0))处的切线方程;
(2)若对任意 ![]() 时,方程g(x)=xf(x)的解的个数,并说明理由.
时,方程g(x)=xf(x)的解的个数,并说明理由.
【答案】
(1)解:由题意得,f(x)=sinx,g(x)=exsinx,
∴g(0)=e0sin0=0;
g'(x)=ex(cosx+sinx),∴g'(0)=1;
故曲线y=g(x)在点(0,g(0))处的切线方程为y=x
(2)解:设H(x)=g(x)﹣xf(x), ![]() ;
;
则当 ![]() 时,
时,
H'(x)=ex(cosx+sinx)﹣sinx﹣xcosx=(ex﹣x)cosx﹣(ex﹣1)sinx,
当 ![]() ,显然有
,显然有 ![]() ;
;
当 ![]() 时,由
时,由 ![]() ,
,
即有 ![]() ,
,
即有H'(x)<0,
所以当 ![]() 时,总有H'(x)<0,
时,总有H'(x)<0,
故H(x)在 ![]() 上单调递减,
上单调递减,
故函数H(x)在 ![]() 上至多有一个零点;
上至多有一个零点;
又 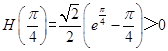 ,
, ![]() ;
;
且H(x)在 ![]() 上是连续不断的,
上是连续不断的,
故函数H(x)在 ![]() 上有且只有一个零点
上有且只有一个零点
【解析】(1)利用导数的几何意义即可求出曲线y=g(x)在点(0,g(0))处的切线方程;(2)构造函数H(x)=g(x)﹣xf(x), ![]() ;利用导数判断函数的单调性,
;利用导数判断函数的单调性,
根据根的存在性定理即可判断函数H(x)在 ![]() 上零点的个数.
上零点的个数.


科目:高中数学 来源: 题型:
【题目】设a>0,b>0( )
A.若lna+2a=lnb+3b,则a>b
B.2a+2a=2b+3b,则a<b
C.若lna﹣2a=lnb﹣3b,则a>b
D.2a﹣2a=2b﹣3b,则a<b
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】f(x)的定义域为(0,+∞),且对一切x>0,y>0都有f![]() =f(x)-f(y),当x>1时,有f(x)>0。
=f(x)-f(y),当x>1时,有f(x)>0。
(1)求f(1)的值;
(2)判断f(x)的单调性并证明;
(3)若f(6)=1,解不等式f(x+3)-f![]() <2;
<2;
(4)若f(4)=2,求f(x)在[1,16]上的值域。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinωx+![]() cosωx的最小正周期为π,x∈R,ω>0是常数.
cosωx的最小正周期为π,x∈R,ω>0是常数.
(1)求ω的值;
(2)若f(![]() +
+![]() )=
)=![]() , θ∈(0,
, θ∈(0,![]() ),求sin2θ.
),求sin2θ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1﹣x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
A.函数f(x)有极大值f(2)和极小值f(1)
B.函数f(x)有极大值f(﹣2)和极小值f(1)
C.函数f(x)有极大值f(2)和极小值f(﹣2)
D.函数f(x)有极大值f(﹣2)和极小值f(2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 过点
过点![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上,过点
上,过点![]() 的直线交圆
的直线交圆![]() 于
于![]() 两点,过点
两点,过点![]() 分别做圆
分别做圆![]() 的切线,记为
的切线,记为![]() .
.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)求证:直线![]() 的交点都在同一条直线上,并求出这条直线的方程.
的交点都在同一条直线上,并求出这条直线的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com