分析:法一(I)连接A
1B,设A
1B∩AB
1=E,连接DE.由ABC-A
1B
1C
1是正三棱柱,且AA
1=AB,知四边形A
1ABB
1是正方形,由此能够证明A
1C∥平面AB
1D.
(II)在面ABC内作DF⊥AB于点F,在面A
1ABB
1内作FG⊥AB
1于点G,连接DG.因为平面A
1ABB
1⊥平面ABC,所以DF⊥平面A
1ABB
1,∠FGD是二面角B-AB
1-D的平面角.由此能求出二面角B-AB
1-D的大小.
(III)因为平面B
1BCC
1⊥平面ABC,且AD⊥BC,所以AD⊥平面B
1BCC
1,又AD?平面AB
1D,所以平面B
1BCC
1⊥平面AB
1D.在平面B
1BCC
1内作CH⊥B
1D交B
1D的延长线于点H,由此能求出点C到平面AB
1D的距离.
解法二:
(I)建立空间直角坐标系D-xyz,连接A
1B,设A
1B∩AB
1=E,连接DE.设A
1A=AB=1,则
D(0,0,0),A1(0,,1),E(-,,),C(,0,0),
=-2,所以A
1C∥DE.由此能够证明A
1C∥平面AB
1D.
(II)由
A(0,,0),B1(-,0,1),知
=(0,,0),=(,0,-1),设n
1=(p,q,r)是平面AB
1D的法向量,
=(
,-1,0),同理,可求得平面AB
1B的法向量是
n2=(,-1,0).由此能求出二面角B-AB
1-D的大小.
(III)平面AB
1D的法向量为n
1=(2,0,1),取其单位法向量
n=(,0,),又=(,0,0).由此能求出点C到平面AB
1D的距离.
解答:解法一(I)证明:
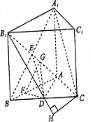
连接A
1B,设A
1B∩AB
1=E,连接DE.
∵ABC-A
1B
1C
1是正三棱柱,且AA
1=AB,
∴四边形A
1ABB
1是正方形,
∴E是A
1B的中点,
又D是BC的中点,
∴DE∥A
1C.…(3分)
∵DE?平面AB
1D,A
1C?平面AB
1D,
∴A
1C∥平面AB
1D.…(4分)
(II)解:在面ABC内作DF⊥AB于点F,
在面A
1ABB
1内作FG⊥AB
1于点G,连接DG.
∵平面A
1ABB
1⊥平面ABC,∴DF⊥平面A
1ABB
1,
∴FG是DG在平面A
1ABB
1上的射影,
∵FG⊥AB
1,∴DG⊥AB
1∴∠FGD是二面角B-AB
1-D的平面角 …(7分)
设A
1A=AB=1,在正△ABC中,DF=
.
在△ABE中,
FG=•BE=,
在Rt△DFG中,
tanFGD==,
所以,二面角B-AB
1-D的大小为
arctan.…(9分)
(III)解:∵平面B
1BCC
1⊥平面ABC,且AD⊥BC,
∴AD⊥平面B
1BCC
1,又AD?平面AB
1D,
∴平面B
1BCC
1⊥平面AB
1D.
在平面B
1BCC
1内作CH⊥B
1D交B
1D的延长线于点H,
则CH的长度就是点C到平面AB
1D的距离.…(12分)
由△CDH∽△B
1DB,得
CH==.
即点C到平面AB
1D的距离是
.…(14分)
解法二:
建立空间直角坐标系D-xyz,如图
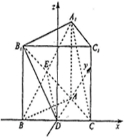
(I)证明:
连接A
1B,设A
1B∩AB
1=E,连接DE.
设A
1A=AB=1,
则
D(0,0,0),A1(0,,1),E(-,,),C(,0,0).∴
=(,-,-1),=(-,,),∴
=-2,
∴A
1C∥DE.…(3分)
∵DE?平面AB
1D,A
1C?平面AB
1D,
∴A
1C∥平面AB
1D.…(4分)
(II)解:∵
A(0,,0),B1(-,0,1),
∴
=(0,,0),=(,0,-1),
设n
1=(p,q,r)是平面AB
1D的法向量,
则
n1•=0,且n1•=0,
故
-q=0,p-r=0.取r=1,得n1=(2,0,1);
同理,可求得平面AB
1B的法向量是
n2=(,-1,0).…(7分)
设二面角B-AB
1-D的大小为θ,
∵
cosθ==,
∴二面角B-AB
1-D的大小为
arccos.…(9分)
(III)解由(II)得平面AB
1D的法向量为n
1=(2,0,1),
取其单位法向量
n=(,0,),又=(,0,0).
∴点C到平面AB
1D的距离
d=|•n|=.…(14分)
点评:本题考查直线和平面平行,求二面角的大小和求点到平面的距离,综合性强,难度大,容易出错.解题时要认真审题,注意转化思想的灵活运用,合理地运用向量法解题.

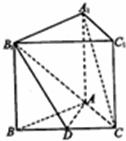 如图,正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1.
如图,正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点.
如图,正三棱柱ABC-A1B1C1各棱长都等于a,E是BB1的中点. (2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(2013•郑州二模)如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点. 如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.
如图,正三棱柱ABC-A1B1C1中(注:底面为正三角形且侧棱与底面垂直),BC=CC1=2,P,Q分别为BB1,CC1的中点.