Question

(21)设直线ay=x－2与抛物线y²=2x交于相异两点A、B,以线段AB为直径作圆H(H为圆心).试证抛物线顶点在圆H的圆周上;并求a的值,使圆H的面积最小.

Answer 1

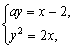
(21)

 解法一：

设A(x_A,y_A),B(x_B,y_B),则其坐标满足

消去x得y²－2ay－4=0.

则

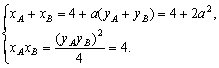
因此·=x_Ax_B+y_Ay_B=0,即OA⊥OB

故O必在圆H的圆周上

又由题意，圆心H(x_H,y_H)是AB的中点，故

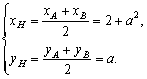
由前已证,OH应是圆H的半径,且

|OH|==,

从而当a=0时,圆H的半径最小,亦使圆H的面积最小.

解法二:设A(x_A,y_A),B(x_B,y_B),则其坐标满足

分别消去x、y得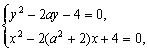

故得A、B所在圆的方程x²+y²－2(a²+2)x－2ay=0.

明显地,O(0,0)满足上面方程.

故A、B、O三点均在上面方程所表示的圆上.

又知A、B中点H的坐标为()=(2+a²,a),

故|OH|=.

而前面圆的方程可表示为

［x－(2+a²)］²+(y－a)²=(2+a²)²+a²,

故|OH|为上面圆的半径R.

从而以AB为直径的圆必过点O(0,0).

又R²=|OH|²=a⁴+5a²+4

故当a=0时,R²最小,从而圆的面积最小.

解法三:

同解法一得O必在圆H的圆周上

又直径|AB|==

=≥=4.

上式当x_A=x_B时,等号成立,直径|AB|最小,从而圆面积最小,此时a=0.