【题目】如图1，在直角梯形
中，AB∥CD，
，且
．现以
为一边向梯形外作正方形
，然后沿边
将正方形翻折，使平面与平面垂直，如图2．
（Ⅰ）求证：BC⊥平面DBE；
（Ⅱ）求点D到平面BEC的距离.
科目：高中数学 来源： 题型：
【题目】已知数据a1，a2，…，an的平均数为a，方差为s2，则数据2a1，2a2，…，2an的平均数和方差分别为( )
A. a，s2 B. 2a，s2
C. 2a，2s2 D. 2a，4s2
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】等差数列{an}的公差d≠0满足
成等比数列，若
=1，Sn是{
}的前n项和，则
的最小值为________．
【答案】4
【解析】
成等比数列，=1，可得：
= 
，即（1+2d）2=1+12d，d≠0，解得d．可得an，Sn．代入利用分离常数法化简后，利用基本不等式求出式子的最小值．
∵成等比数列，a1=1，
∴= ，
∴（1+2d）2=1+12d，d≠0，
解得d=2．
∴an=1+2（n﹣1）=2n﹣1．
Sn=n+
×2=n2．
∴=
=n+1+
﹣2≥2
﹣2=4，
当且仅当n+1=时取等号，此时n=2，且取到最小值4，
故答案为：4．
【点睛】
本题考查了等差数列的通项公式、前n项和公式，等比中项的性质，基本不等式求最值，在利用基本不等式求最值时，要特别注意“拆、拼、凑”等技巧，使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用，否则会出现错误.
【题型】填空题
【结束】
17
【题目】设
是公比为正数的等比数列,
,
(1)求的通项公式;
(2)设
是首项为1,公差为2的等差数列,求数列
的前
项和
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在△ABC中，∠C=60°，D是BC上一点，AB=31，BD=20，AD=21．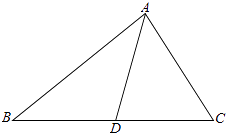 
（1）求cos∠B的值；
（2）求sin∠BAC的值和边BC的长．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，已知直线l的参数方程为 
（t为参数，0＜α＜π），以原点O为极点，以x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ= 
（p＞0）．
（Ⅰ）写出直线l的极坐标方程和曲线C的直角坐标方程；
（Ⅱ）若直线l与曲线C相交于A，B两点，求 
+ 
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在直角坐标系
中，圆
与
轴负半轴交于点
，过点
的直线
，
分别与圆
交于
，
两点．
（1）若
，
，求△
的面积；
（2）过点
作圆O的两条切线，切点分别为E，F，求
；
（3）若
，求证：直线
过定点．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，ABCD是正方形，O是正方形的中心，PO⊥底面ABCD，E是PC的中点．
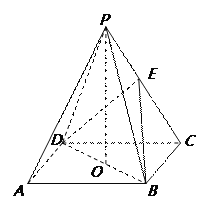
.求证：（Ⅰ）PA∥平面BDE；（Ⅱ）平面PAC⊥平面BDE；(III)若PB与底面所成的角为600, AB=2a,求三棱锥E-BCD的体积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，
是东西方向的公路北侧的边缘线，某公司准备在上的一点
的正北方向的
处建设一仓库，设
，并在公路北侧建造边长为
的正方形无顶中转站
（其中
在上），现从仓库向和中转站分别修两条道路
，已知
，且
．
（1）求
关于
的函数解析式，并求出定义域；
（2）如果中转站四堵围墙造价为10万元
，两条道路造价为30万元，问：取何值时，该公司建设中转站围墙和两条道路总造价
最低．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲、乙两校各有3名教师报名支教，期中甲校2男1女，乙校1男2女．
（1）若从甲校和乙校报名的教师中各任选1名，写出所有可能的结果，并求选出的2名教师性别相同的概率；
（2）若从报名的6名教师中任选2名，写出所有可能的结果，并求选出的2名教师来自同一学校的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
