
 =(2x-y+1,x+y-2),
=(2x-y+1,x+y-2), =(2,-2),①当x、y为何值时,
=(2,-2),①当x、y为何值时, 与
与 共线?②是否存在实数x、y,使得
共线?②是否存在实数x、y,使得 ⊥
⊥ ,且|
,且| |=|
|=| |?若存在,求出xy的值;若不存在,说明理由.
|?若存在,求出xy的值;若不存在,说明理由. 和
和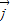 是两个单位向量,其夹角是90°,
是两个单位向量,其夹角是90°, ,若
,若 ,求实数k的值.
,求实数k的值.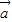 与
与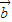 共线,可得存在非零实数λ使得
共线,可得存在非零实数λ使得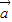 =λ
=λ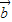 ,从而可得结论;
,从而可得结论;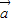 ⊥
⊥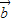 得,(2x-y+1)×2+(x+y-2)×(-2)=0,由|
得,(2x-y+1)×2+(x+y-2)×(-2)=0,由|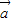 |=|
|=|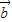 |得,(2x-y+1)2+(x+y-2)2=8,从而可得结论;
|得,(2x-y+1)2+(x+y-2)2=8,从而可得结论;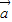 与
与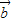 共线,
共线,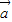 =λ
=λ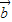 ,
,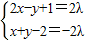
 ,y∈R;
,y∈R;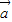 ⊥
⊥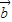 得,(2x-y+1)×2+(x+y-2)×(-2)=0
得,(2x-y+1)×2+(x+y-2)×(-2)=0 |=|
|=| |得,(2x-y+1)2+(x+y-2)2=8.(ii)
|得,(2x-y+1)2+(x+y-2)2=8.(ii) 或
或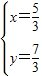 ;
;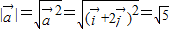 ,①
,①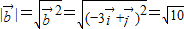 ,②
,②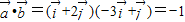 ③…(10分)
③…(10分)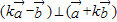 ,
,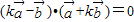 ,得,
,得,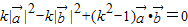
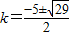 …(14分)
…(14分)

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| i |
| j |
| a |
| i |
| j |
| b |
| i |
| j |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| n |
| m |
| a |
| m |
| n |
| m |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
(2)已知函数f(x)满足f(x+y)+f(x-y)=2f(x)·f(y),且f(0)≠0,若f(![]() )=0,求f(π)及f(2π).
)=0,求f(π)及f(2π).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com