
已知 都是正数,
都是正数,
(1)若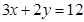 ,求
,求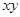 的最大值
的最大值
(2)若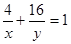 ,求
,求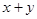 的最小值.
的最小值.
(1)6;(2)36.
解析试题分析:(1)直接利用基本不等式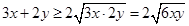 ,
,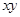 的最大值随之而定;(2)如果直接利用基本不等式则有
的最大值随之而定;(2)如果直接利用基本不等式则有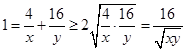 ①,
①,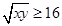 ,因此
,因此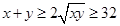 ②,这样就可能得出
②,这样就可能得出 的最小值为32,实际上这个最小值是取不到的,因为不等式①取等号的条件是
的最小值为32,实际上这个最小值是取不到的,因为不等式①取等号的条件是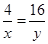 ,
,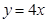 ,不等式②取等号的条件是
,不等式②取等号的条件是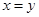 ,即不等式①②不能同时取等号,故
,即不等式①②不能同时取等号,故 的最小值不是32.正确的解法是把
的最小值不是32.正确的解法是把 看作
看作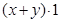 ,把其中的1用已知
,把其中的1用已知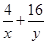 代换,即
代换,即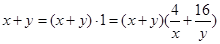 ,展开后就可以直接利用基本不等式求出结果.
,展开后就可以直接利用基本不等式求出结果.
试题解析:(1)xy=·3x·2y≤2=6 4分
当且仅当即时取“=”号.
所以当x=2,y=3时,xy取得最大值6 ..6分
(2)由 且
且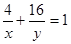 得
得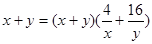

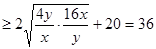 , ..10分
, ..10分
当且仅当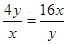 ,即x=12且y=24时,等号成立,
,即x=12且y=24时,等号成立,
所以x+y的最小值是36 12分
考点:基本不等式的应用.


科目:高中数学 来源: 题型:解答题
阅读:
已知 、
、 ,
, ,求
,求 的最小值.
的最小值.
解法如下: ,
,
当且仅当 ,即
,即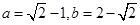 时取到等号,
时取到等号,
则 的最小值为
的最小值为 .
.
应用上述解法,求解下列问题:
(1)已知 ,
, ,求
,求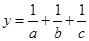 的最小值;
的最小值;
(2)已知 ,求函数
,求函数 的最小值;
的最小值;
(3)已知正数 、
、 、
、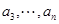 ,
, ,
,
求证: .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 的定义域为
的定义域为 . 设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.
. 设点P是函数图象上的任意一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M、N.
(1)求证: 是定值;
是定值;
(2)判断并说明 有最大值还是最小值,并求出此最大值或最小值.
有最大值还是最小值,并求出此最大值或最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本y(万元)与年产量x(吨)之间的函数关系式可以近视地表示为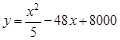 ,已知此生产线的年产量最大为210吨.
,已知此生产线的年产量最大为210吨.
(Ⅰ) 求年产量为多少吨时,生产每吨产品的平均成本最低,并求最低成本;
(Ⅱ)若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
若a>0,b>0,a+b=2,则下列不等式对一切满足条件的a,b恒成立的是 (写出所有正确命题的编号).
①ab≤1; ② +
+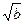 ≤
≤ ; ③a2+b2≥2;
; ③a2+b2≥2;
④a3+b3≥3; 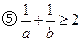 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com