
①直线y=kx+1与椭圆![]() =1总有两个交点;
=1总有两个交点;
②函数f(x)=2sin(3x-![]() )的图像可由函数f(x)=2sin3x按向量a=(-
)的图像可由函数f(x)=2sin3x按向量a=(-![]() ,0)平移得到;
,0)平移得到;
③函数f(x)=|x2-2ax+b|一定是偶函数;
④抛物线x=ay2(a≠0)的焦点坐标是(![]() ,0).
,0).
回答以上4个命题中,真命题是_______________(写出所有真命题的编号).
①④
解析:此题是多项选择题,涉及内容较多,包括圆锥曲线、三角函数、函数的性质等内容.
①法一是根据直线y=kx+1过定点(0,1),点(0,1)在椭圆![]() =1内部,所以直线y=kx+1与椭圆
=1内部,所以直线y=kx+1与椭圆![]() =1恒有两个公共点.
=1恒有两个公共点.
法二根据方程组 可得(2+k2)x2+2kx-3=0,
可得(2+k2)x2+2kx-3=0,
由△=4k2+12(2+k2)=16k2+24>0可知,方程有两根,即直线y=kx+1与椭圆![]() =1恒有两个公共点.
=1恒有两个公共点.
②设函数f(x)=2sin3x按a=(m,n)平移后得到y+n=2sin(3x+3m-![]() ),
),
令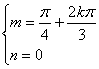 求得a=(
求得a=(![]() ,0).
,0).
③f(x)=|x2-2ax+b| ∴f(-x)=|x2+2ax+b|
∵当a=0时,f(-x)=f(x),所以为偶函数;
当a≠0时,f(-x)≠f(x),所以不为偶函数.
④x=ay2即y2=![]() x,所以抛物线焦点坐标为(
x,所以抛物线焦点坐标为(![]() ,0).
,0).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:阅读理解
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:022
(2006
江西九校模拟)请阅读下列命题:A.直线
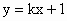 与椭圆
与椭圆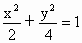 总有两个交点;
B.
总有两个交点;
B. 的图象可由f(x)=2sin3x按向量
的图象可由f(x)=2sin3x按向量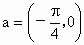 平移得到;
平移得到;
C.在
R上连续的函数f(x)若是增函数,则对于任意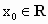 ,均有,
,均有,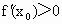 成立;
成立;
D.抛物线
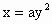 (a≠0)的焦点坐标是(
(a≠0)的焦点坐标是(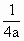 ,0).
,0).
以上
4个命题中,真命题是________(按照原顺序写出所有真命题的代号).查看答案和解析>>
科目:高中数学 来源: 题型:
① 直线y=kx+1与椭圆![]() 总有两个交点;
总有两个交点;
② f(x)=2sin(3x-![]() )的图像可由f(x)=2sin3x按向量a=(-
)的图像可由f(x)=2sin3x按向量a=(-![]() ,0)平移得到;
,0)平移得到;
③ 在R上连续的函数f(x)若是增函数,则对于任意x0∈ R,均有![]() (x0)>0成立;
(x0)>0成立;
④ 抛物线x=ay2(a≠0)的焦点坐标是(![]() ,0);
,0);
以上4个命题中,真命题是____________(写出所有真命题的编号).
查看答案和解析>>
科目:高中数学 来源:2010年福建省高三模拟考试数学(理科)试题 题型:填空题
请阅读下列材料:对命题“若两个正实数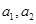 满足
满足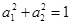 ,那么
,那么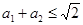 。”
。”
证明如下:构造函数 ,因为对一切实数
,因为对一切实数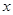 ,恒有
,恒有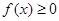 ,又
,又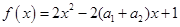 ,从而得
,从而得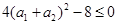 ,所以
,所以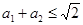 。根据上述证明方法,若
。根据上述证明方法,若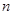 个正实数满足
个正实数满足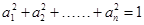 时,你可以构造函数
时,你可以构造函数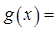 ,进一步能得到的结论为
。(不必证明)
,进一步能得到的结论为
。(不必证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com