Question

在10件产品中，有3件一等品，4件二等品，3件三等品。从这10件产品中任取3件，求：

（I） 取出的3件产品中一等品件数X的分布列和数学期望；

（II） 取出的3件产品中一等品件数多于二等品件数的概率。 

 

Answer 1

【答案】

（Ⅰ）解：由于从10件产品中任取3件的结果为，从10件产品中任取3件，其中恰有k件一等品的结果数为，那么从10件产品中任取3件，其中恰有k件一等品的概率为P(X=k)= ,k=0,1,2,3.

所以随机变量X的分布列是

X	0	1	2	3
P

X的数学期望EX=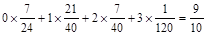

（Ⅱ）解：设“取出的3件产品中一等品件数多于二等品件数”为事件A，“恰好取出1件一等品和2件三等品”为事件A₁“恰好取出2件一等品“为事件A₂，”恰好取出3件一等品”为事件A₃由于事件A₁，A₂，A₃彼此互斥，且A=A₁∪A₂∪A₃而

P(A₂)=P(X=2)= 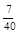,P(A3)=P(X=3)= ,

所以取出的3件产品中一等品件数多于二等品件数的概率为

P(A)=P(A₁)+P(A₂)+P(A₃)= ++=

 

【解析】略