
(1)求直线AC与平面PAB所成角的大小;
(2)在射线CP上确定一点Q,求CQ为多少时,能使二面角D-AQ-B的度数为θ,且cosθ=![]() .
.
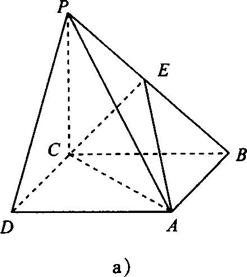
第18题图
答案:(1)解法一:过点C作为CE⊥PB,垂足为E,连接AE、EC、AC,如图a所示.
∵AB⊥PC,AB⊥BC,
∴AB⊥平面PBC,平面PAB⊥平面PBC,
故CE⊥平面PAB,∠EAC为所求的角
在Rt△AEC中,EC=![]() ,AC=
,AC=![]() ,∴∠EAC=
,∴∠EAC=![]() .
.

第18题图
解法二:分别以直线CD,CB,CP为x轴,y轴,z轴建立空间直角坐标系C-xyz,![]() =(1,1,0),
=(1,1,0),![]() =(-1,0,0),
=(-1,0,0),![]() =(0,1,-1),设n=(x,y,z)为平面PAB的一个法向量,则
=(0,1,-1),设n=(x,y,z)为平面PAB的一个法向量,则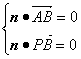 ,∴
,∴![]() ,∴
,∴![]() ,取y=1.
,取y=1.
∴n=(0,1,1).设直线AC与平面PAB所成的二面角为θ,则sinθ=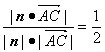 ,θ=
,θ=![]() .
.
(2)解法一:如图b所示,过点B作BF⊥QA,垂足为F,
连接FD,BD;
∵△QAB≌△QAO,FD⊥QA,
∴∠BFD是二面角D-QA-B的平面角
设QC=x,则FD=FB=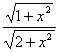 ,
,
cos∠DFB=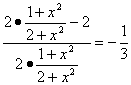 ,解得x=
,解得x=![]() 即为所求的CQ的长.
即为所求的CQ的长.
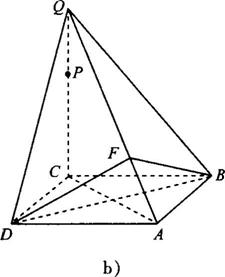
第18题图(续)
解法二:设:Q(0,0,t),m=(x,y,z)为平面QAD的一个法向量,![]() =(0,1,0),
=(0,1,0),![]() =(-1,0,t).
=(-1,0,t).
由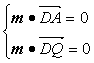 ,得
,得![]()
取x=1,∴m=(1,0,![]() );
);
同理,平面QAB的一个法向量n=(0,1,![]() ).
).
|cosθ|=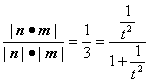 ,解得t=
,解得t=![]() .
.


 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源: 题型:
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,BC=
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,BC=| 2 |
| AE |
| AP |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,AD=
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,AD=| 3 |
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=2
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=2| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com